无题
CTF中的LFSR类题目
题型:给出反馈函数和输出序列,反推出初始状态
2018 CISCN 线上赛 oldstreamgame
题目
flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14
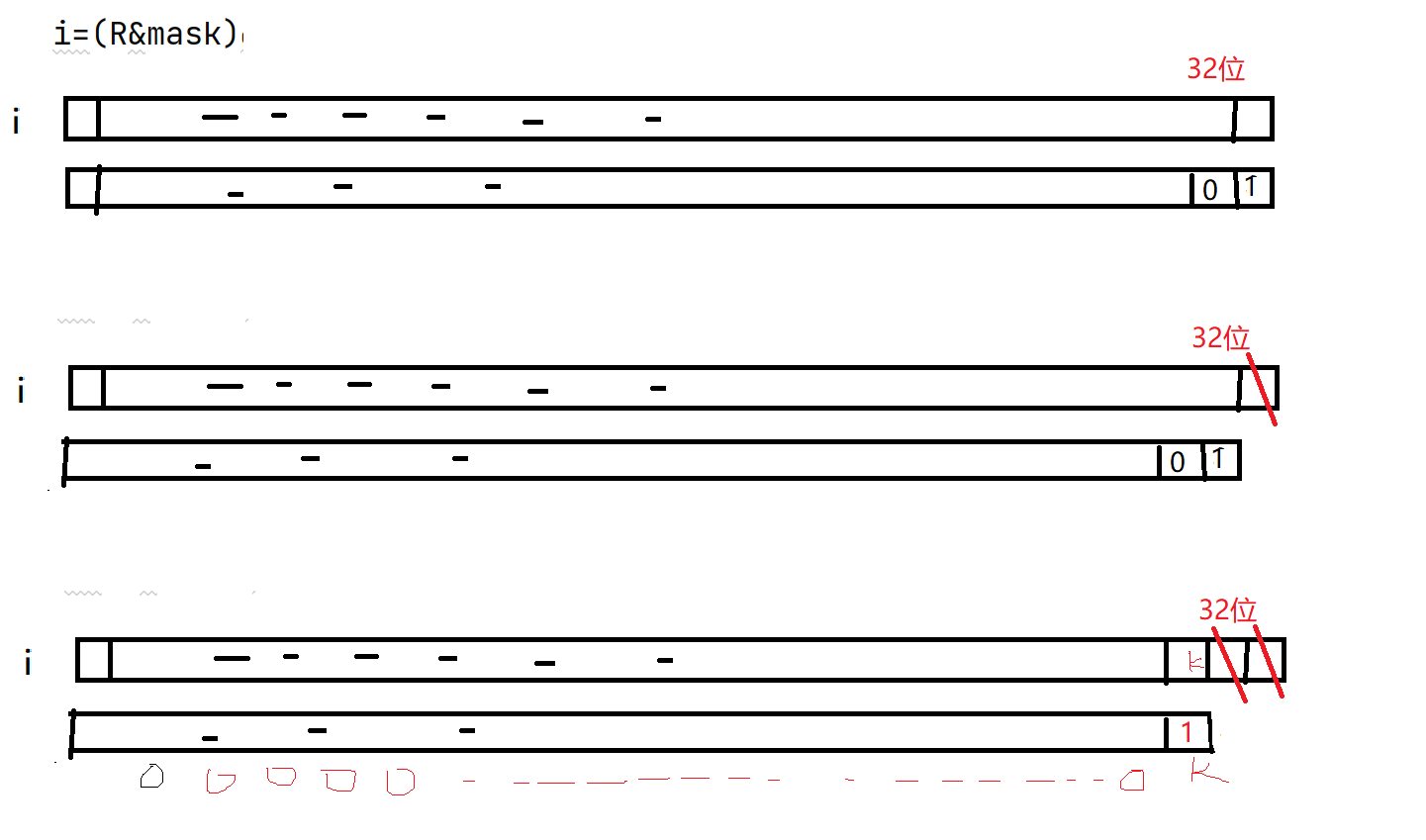
def lfsr(R,mask):
#0xffffffff -->32位 '0b101100100000011110110001
output = (R << 1) & 0xffffffff
i=(R&mask)&0xffffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
#将提取的子字符串解析为一个十六进制数,并将其转换为对应的整数类型。
R=int(flag[5:-1],16)
mask = 0b10100100000010000000100010010100
#0b11111111111111111111111111111111'(0xffffffff前32位)
# 00010110000011111011100101001010
f=open("key","w")
for i in range(100):
tmp=0
for j in range(8):
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out
f.write(chr(tmp))# #将lfsr输出的序列每8个二进制为一组,转化为字符,共12组
f.close()
题解
0xffffffff -->32位的常数 按位与运算(同1才为1)与做按与运算,结果为原数低32位,
R(flag)是32位的初始状态
output = (R << 1) & 0xffffffff 把R左移一位后低32位(即抹去R的最高位)
i=(R&mask)&0xffffffff
#把传入的R和mask做按位与运算,运算结果取低32位,将该值赋给i变量。
#从i的最低位向i的最高位依次做异或运算,将运算结果赋给lastbit变量。
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
i&1的作用是从低到高取出每一位
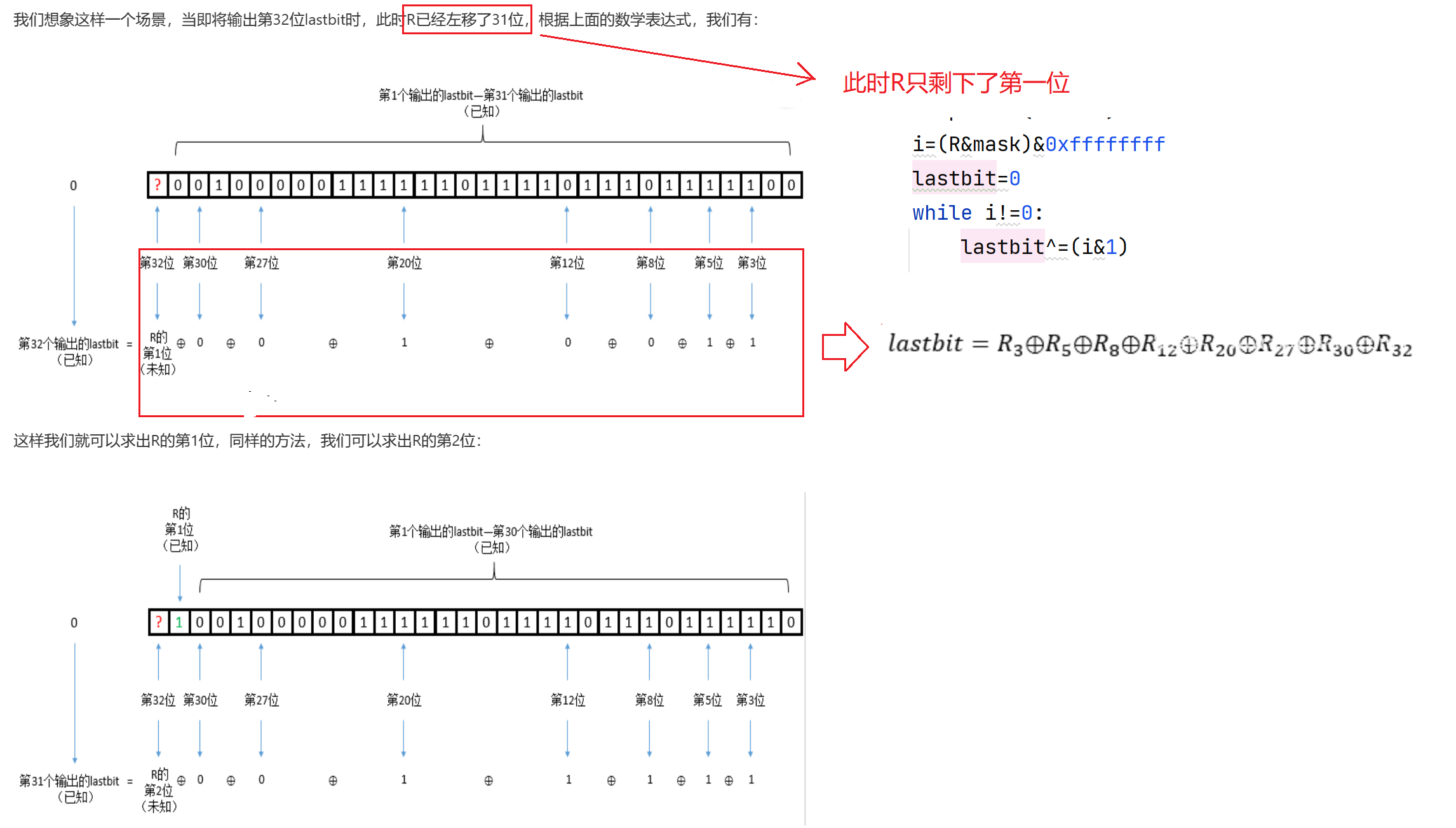
lastbit^=(i&1)说明Lastbit是i从低位异或到高位的结结果,如果i中有奇数个1,结果1;偶数个1,结果为0。
output^=lastbit将output变量的最后一位设置成lastbit变量的值。
整体流程:
$
(从右边数
每轮产生一个结果,
WP
f = open('key.txt','rb').read()
r = bytes_to_long(f)
bin_out = bin(r)[2:].zfill(12*8)
R = bin_out[:19] #获取输出序列中与掩码msk长度相同的值
mask = '10100100000010000000100010010100'
key = '00100000111111011110111011111000'
tmp=key
R = ''
for i in range(32):
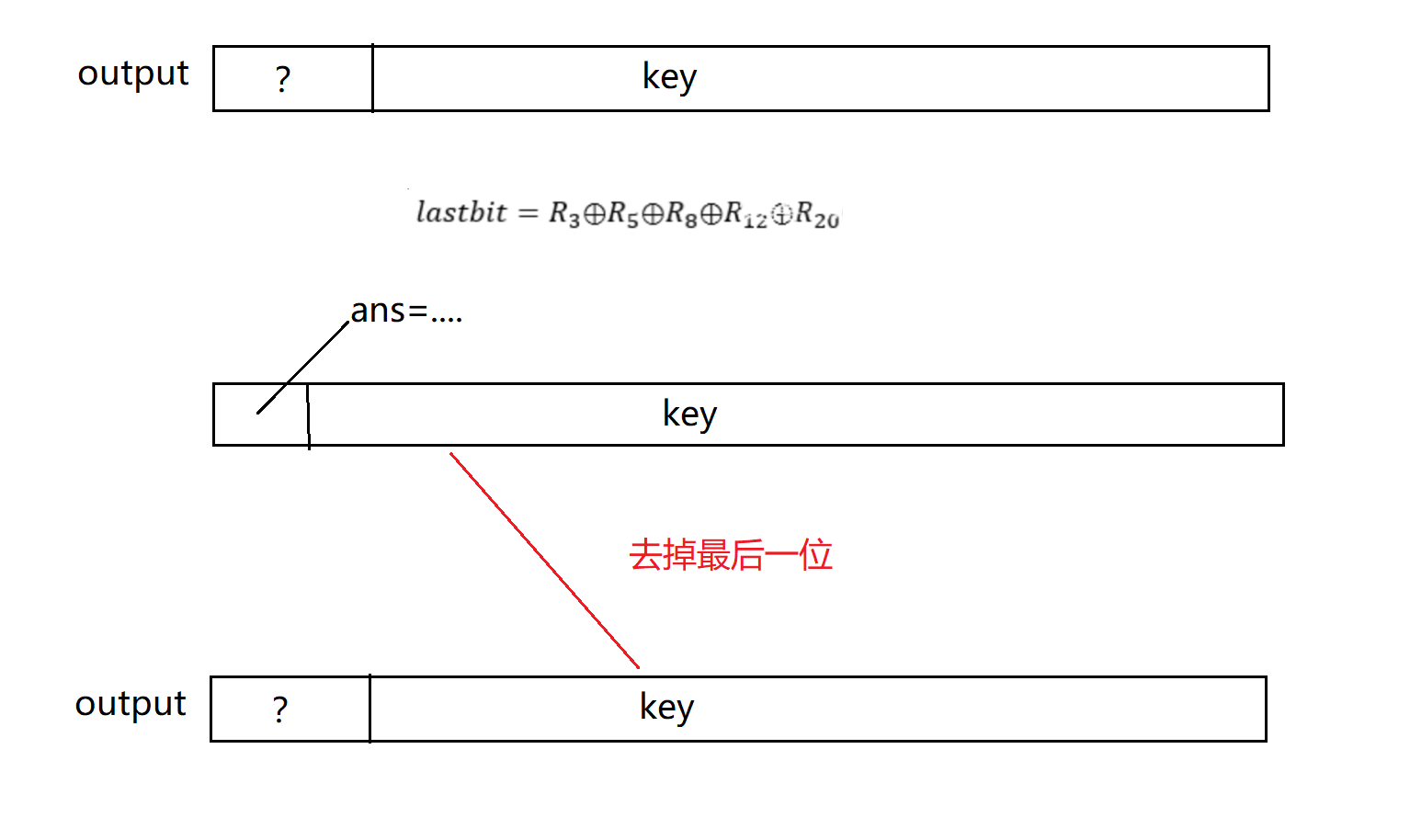
output = '?' + key[:31]
ans = int(key2[-1-i])^int(output[-3])^int(output[-5])^int(output[-8])^int(output[-12])^int(output[-20])^int(output[-27])^int(output[-30])
R += str(ans)
key = str(ans) + key[:31]
R = format(int(R[::-1],2),'x')
flag = "flag{" + R + "}"
print flag2018 强网杯 线上赛 streamgame1
题目
from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag) == 25
def lfsr(R, mask):
output = (R << 1) & 0xffffff
i = (R & mask) & 0xffffff
lastbit = 0
while i != 0:
lastbit ^= (i & 1)
i = i >> 1
output ^= lastbit
return (output, lastbit)
R = int(flag[5:-1], 2)
mask = 0b1010011000100011100
f = open("key", "ab")
for i in range(12):
tmp = 0
for j in range(8):
(R, out) = lfsr(R, mask)
tmp = (tmp << 1) ^ out
f.write(chr(tmp))
f.close()
题解
方法一
和第一题一样
方法二
因为flag不是很长(19bit),所以可以爆破
WP
#方法一
from Crypto.Util.number import*
f = open('key.txt','rb').read()
r = bytes_to_long(f)
bin_out = bin(r)[2:].zfill(12*8)
R = bin_out[:19] #获取输出序列中与掩码msk长度相同的值
print(R)
mask = '1010011000100011100'
key = '0101010100111000111'
R = ''
for i in range(19):
output = 'x'+key[:18]
out = int(key[-1])^int(output[-3])^int(output[-4])^int(output[-5])^int(output[-9])^int(output[-13])^int(output[-14])^int(output[-17])
R += str(out)
key = str(out)+key[:18]
print('flag{'+R[::-1]+'}')
#方法二
from Crypto.Util.number import*
import os,sys
os.chdir(sys.path[0])
f = open('key.txt','rb').read()
c = bytes_to_long(f)
bin_out = bin(c)[2:].zfill(12*8) #将key文本内容转换为 2 进制数,每个字节占 8 位
R = bin_out[0:19] #取输出序列的前19位
mask = 0b1010011000100011100
def lfsr(R,mask):
output = (R << 1) & 0xffffffff
i=(R&mask)&0xffffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
#根据生成规则,初始状态最后一位拼接输出序列
#我们可以猜测seed的第19位(0或1),如果seed19+R[:18]输出值等于R[:19],那么就可以确定seed值了
def decry():
cur = bin_out[0:19] #前19位 2 进制数
res = ''
for i in range(19):
if lfsr(int('0'+cur[0:18],2),mask)[0] == int(cur,2):
res += '0'
cur = '0'+cur[0:18]
else:
res += '1'
cur = '1' + cur[0:18]
return int(res[::-1],2)
r = decry()
print(bin(r))
2018 强网杯 线上赛 streamgame2
题目
from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==27
def lfsr(R,mask):
output = (R << 1) & 0xffffff
i=(R&mask)&0xffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
R=int(flag[5:-1],2)
mask=0x100002
f=open("key","ab")
for i in range(12):
tmp=0
for j in range(8):
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out
f.write(chr(tmp))
f.close()题解
同1,2,len(flag)==27
WP
from Crypto.Util.number import*
bin_out = open('key.txt','rb').read()
key = bin(bytes_to_long(bin_out))[2:]
# print(key[0:21])
# print(bin(int('0x100002',16)))
key = '101100101110100100001'
mask= '100000000000000000010'
R = ''
for i in range(21):
output = '?' + key[:20]
ans = int(key[-1]) ^ int(output[-2])
R += str(ans)
key = str(ans) + key[:20]
print(R[::-1])
2019 0CTF/TCTF 线上赛 zer0lfsr
题目
from secret import init1,init2,init3,FLAG
import hashlib
assert(FLAG=="flag{"+hashlib.sha256(init1+init2+init3).hexdigest()+"}")
class lfsr():
def __init__(self, init, mask, length):
self.init = init
self.mask = mask
self.lengthmask = 2**(length+1)-1
def next(self):
nextdata = (self.init << 1) & self.lengthmask
i = self.init & self.mask & self.lengthmask
output = 0
while i != 0:
output ^= (i & 1)
i = i >> 1
nextdata ^= output
self.init = nextdata
return output
def combine(x1,x2,x3):
return (x1*x2)^(x2*x3)^(x1*x3)
if __name__=="__main__":
l1 = lfsr(int.from_bytes(init1,"big"),0b100000000000000000000000010000000000000000000000,48)
l2 = lfsr(int.from_bytes(init2,"big"),0b100000000000000000000000000000000010000000000000,48)
l3 = lfsr(int.from_bytes(init3,"big"),0b100000100000000000000000000000000000000000000000,48)
with open("keystream","wb") as f:
for i in range(8192):
b = 0
for j in range(8):
b = (b<<1)+combine(l1.next(),l2.next(),l3.next())
f.write(chr(b).encode())题解
方法一:Fast Correlation Attacks
Fast Correlation Attacks(快速相关攻击)
深入分析CTF中的LFSR类题目(二)-安全客 - 安全资讯平台 (anquanke.com)
Correlation Attacks(相关攻击)
利用单个LFSR的输出序列和combine之后的LFSR的输出序列之间具有的一定的相关性这一特点,来还原LFSR的初始状态
两种重要的快速相关攻击的手法:Algorithm A和Algorithm B
使用该攻击的满足条件:单个LFSR的输出序列和combine之后的LFSR的输出序列之间的相关性大于0.53\
例子:
| x1 | x2 | x3 | combine(x1,x2,x3) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
当x1=0时,会对应四个result(即combine(x1,x2,x3))值,其中3个result值为0,一个为1,即x1和result相同的概率为0.75。同理,x2和x3也满足这一规律,这样一来我们就找到了一个很关键的要素,那就是单个x的值和combine之后的值相同的概率有0.75。
Meier-Staffelbach模型
两种重要的快速相关攻击的手法:Algorithm A和Algorithm B,都默认建立在该模型之下。
两种算法的比较:
1.算法A:
优点:错误率接近0.75时攻击效果显著。
缺点:当抽头数量较多时,该攻击将逐渐退化为穷举攻击。
2.算法B:
优点:错误率接近0.5时攻击效果显著。
缺点:该攻击需要进行大量的双精度计算,计算量较大
脚本:
BLOCK = 48
class LFSR:
def __init__(self, init, mask, length=BLOCK):
self.init = init
self.length = length
self.lengthmask = 2 ** length - 1
self.mask = mask & self.lengthmask
def next(self):
nextdata = (self.init << 1) & self.lengthmask
output = parity(self.init & self.mask)
nextdata ^= output
self.init = nextdata
return output
def step_back(self):
output = self.init & 1
predata = self.init >> 1
high_bit = parity(predata & self.mask) ^ output
self.init = (high_bit << (self.length - 1)) | predata
def parity(x):
res = 0
while x:
x -= x & (-x)
res ^= 1
return res
def get_data():
data = open("keystream", "rb").read().decode()
result = []
for i in range(len(data)):
x = ord(data[i])
for j in range(8):
result.append((x >> (7 - j)) & 1)
return tuple(result)
def bit_stream_to_int(a):
return int(''.join(map(str, a)), 2)
def S(p, t):
if t == 1:
return p
return p * S(p, t - 1) + (1 - p) * (1 - S(p, t - 1))
def C(n, m):
if n < m:
return 0
if m > n / 2:
m = n - m
res = 1
for i in range(m):
res *= n - i
for i in range(m):
res //= i + 1
return res
def calc_eq(loc, mask, z, n, p):
l = len(z)
t = 0
tap = [n]
for i in range(n):
if (mask >> i) & 1:
tap.append(n - i - 1)
t += 1
tap.reverse()
eqs = [tap]
while True:
if (tap[-1] << 1) >= l:
break
tmp = [0] * len(tap)
for i in range(len(tap)):
tmp[i] = tap[i] << 1
eqs.append(tmp)
tap = tmp
shift_eqs = []
for eq in eqs:
for i in range(len(eq)):
offset = loc - eq[i]
if eq[0] + offset < 0 or eq[-1] + offset >= l:
continue
tmp = [0] * len(eq)
for j in range(len(eq)):
tmp[j] = eq[j] + offset
shift_eqs.append(tmp)
m = len(shift_eqs)
if m == 0:
return 0, 0, 0
h = 0
for eq in shift_eqs:
# print(eq)
xor_sum = 0
for i in eq:
xor_sum ^= z[i]
if xor_sum == 0:
h += 1
s = S(p, t)
p1 = C(m, h) * pow(s, h) * pow(1 - s, m - h)
p0 = C(m, h) * pow(s, m - h) * pow(1 - s, h)
return m, h, p1 / (p1 + p0)
def gen_linear_eq(mask, n, length):
length = max(length, n)
tap = []
for i in range(n):
if (mask >> i) & 1:
tap.append(i + 1)
eqs = []
for i in range(n):
eqs.append(1 << i)
for i in range(n, length):
res = 0
for j in tap:
res ^= eqs[i - j]
eqs.append(res)
return eqs
def solve(assume, n):
eq_len = len(assume)
mat = []
for i in range(eq_len):
mat.append([0] * n)
b = [0] * eq_len
for i in range(eq_len):
b[i] = assume[i][1]
for j in range(n):
mat[i][j] = (assume[i][0] >> j) & 1
for i in range(n):
tmp = -1
for j in range(i, eq_len):
if mat[j][i]:
tmp = j
break
if tmp == -1:
return []
mat[tmp], mat[i] = mat[i], mat[tmp]
b[tmp], b[i] = b[i], b[tmp]
for j in range(eq_len):
if not mat[j][i] or i == j:
continue
b[j] ^= b[i]
for k in range(i, n):
mat[j][k] ^= mat[i][k]
if not any(mat[n - 1]):
return []
print(b[:n])
return b[:n]
def get_init_stat(locs, linear_eq, mask, n, z):
assume = [(linear_eq[x[0]], x[1]) for x in locs]
b = []
idx = n
print("----- try solve equations -----")
while not b: # try again if linear correlation
b = solve(assume[:idx], n)
idx += 1
print("----- solve success -----")
stat = bit_stream_to_int(b)
print("----- genrate original LFSR -----")
l = LFSR(stat, mask, n)
for i in range(n):
l.step_back()
init_stat = l.init
print("init:", init_stat)
print("----- genrate original LFSR finished -----")
z_new = []
same_cnt = 0
for i in range(len(z)):
z_new.append(l.next())
same_cnt += int(z[i] == z_new[i])
for loc in locs[:idx]:
assert(z_new[loc[0]] == loc[1])
print("match rate:", same_cnt / len(z))
return init_stat
def crack(mask, n, z, p):
print("----- select candidates -----")
candidates = []
for i in range(len(z)):
m, h, p_star = calc_eq(i, mask, z, n, p)
tmp = (p_star, i, m, h)
candidates.append(tmp)
candidates.sort(reverse=True)
print(candidates[:5])
print("----- select candidates finished -----")
linear_eq = gen_linear_eq(mask, BLOCK, len(z))
locs = [(cand[1], z[cand[1]]) for cand in candidates]
return get_init_stat(locs, linear_eq, mask, n, z)
if __name__ == "__main__":
z = get_data()
mask = 0b100000000000000000000000010000000000000000000000
init1 = crack(mask, BLOCK, z, 0.75)
mask = 0b100000000000000000000000000000000010000000000000
init2 = crack(mask, BLOCK, z, 0.75)
mask = 0b100000100000000000000000000000000000000000000000
init3 = crack(mask, BLOCK, z, 0.75)
init = [init1, init2, init3]
print(init)
#根据反馈函数在进行flag的求解
for i in range(len(init)):
init[i] = bytes.fromhex(hex(init[i])[2:])
init_bytes = b""
for i in init:
init_bytes += i
import hashlib
print("flag{" + hashlib.sha256(init_bytes).hexdigest() + "}")方法二:z3约束求解
z3约约束求解的核心是列方程和解方程,如果能解,z3就会给你一组解(注意:如果方程有多组解,z3只会给你其中的一组解,所以这组解虽然满足题意但未必是正确答案,这个时候我们可以尝试能否继续为方程添加约束条件,进一步限制解的范围,从而获得我们预期的一组解)
#声明,inter1未知数
init1 = BitVec('init1', 48)
s = Solver()
s.add(outputs[i] == combine(l1.next(), l2.next(), l3.next()))Solver添加方程的时候,只添加了200个方程,按理来讲,我们应该有len(outputs)个方程,为什么只添加200个呢?实际上在这里200并不是一个精确数字,而是一个大概的数字,意思是当添加够200个方程的时候,得到的解就已经固定了,即我们需要的那组解,我们把它改到300,得到的还是这组解,所以就不用继续添加没有必要的方程了。那么既然我们说反正都一样,我直接给他添加len(outputs)个方程,不是更省事吗,也不用去关它多少个方程之后解就固定了,其实大家可以动手去试一下,这样虽然理论上是一样的,但是实际操作的时候计算机反而解不出来,原因就是约束的方程过多了,计算机反而解不出来了,因此我们需要手动测试一下,找到一个合适的数值,来使得我们的脚本既能求出我们希望的一组解,又能让计算机正常跑出来。
wp
from z3 import *
class lfsr():
def __init__(self, init, mask, length):
self.init = init
self.mask = mask
self.lengthmask = 2**(length+1)-1
self.length = length
def next(self):
nextdata = (self.init << 1) & self.lengthmask
i = self.init & self.mask & self.lengthmask
output = 0
for j in range(self.length):
output ^= (i & 1)
i = i >> 1
nextdata ^= output
self.init = nextdata
return output
def combine(x1,x2,x3):
return (x1*x2)^(x2*x3)^(x1*x3)
init1 = BitVec('init1', 48)
init2 = BitVec('init2', 48)
init3 = BitVec('init3', 48)
l1 = lfsr(init1, 0b100000000000000000000000010000000000000000000000, 48)
l2 = lfsr(init2, 0b100000000000000000000000000000000010000000000000, 48)
l3 = lfsr(init3, 0b100000100000000000000000000000000000000000000000, 48)
#创建一个解的声明对象
s = Solver()
with codecs.open('keystream', 'rb', 'utf8') as f:
keystream = f.read()
outputs = []
for i in keystream:
a = ord(i)
b = '0'*(8 - len(bin(a)[2:])) + bin(a)[2:]
for j in b:
outputs.append(int(j))
for i in range(200):
#添加条件(即方程)
s.add(outputs[i] == combine(l1.next(), l2.next(), l3.next()))
#判断是否有解:
s.check()
print(s.model())
解出init1,init2,init3
2018 强网杯 线上赛 streamgame3
题目
from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==27
def nlfsr(R,mask):
output = (R << 1) & 0xffffff
i=(R&mask)&0xffffff
lastbit=0
changesign=True
while i!=0:
if changesign:
lastbit &= (i & 1)
changesign=False
else:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
R=int(flag[5:-1],2)
mask=0b110110011011001101110
f=open("key","ab")
for i in range(1024*1024):
tmp=0
for j in range(8):
(R,out)=nlfsr(R,mask)
tmp=(tmp << 1)^out
f.write(chr(tmp))
f.close()【复现】强网杯-StreamGame3-Writeup – Rhy7hm (rhythmmark.github.io)
Fast Correlation Attacks(快速相关攻击)