流密码（Stream cipher）

流密码 | Lazzaro (lazzzaro.github.io)

密码学复习——第二章（流密码）-阿里云开发者社区 (aliyun.com)

(144条消息) 流密码（一次一密、流密码/序列密码、LFSR、RC4)_Yongliang Xu的博客-CSDN博客

  • 明文逐位与密钥流进行异或运算，生成密文流
  • 又称序列密码
  • 对称加密算法，加密和解密双方使用相同伪随机加密数据流（pseudo-random stream）作为密钥
  • 流密码的安全性依赖于生成高质量的密钥流。
  • 密钥流应该是伪随机的，不可预测的，并且对于同一个密钥，不应该重复出现。

二元加法流密码

一种基于二进制加法运算的流密码算法。它使用一个密钥流和明文流进行逐位的二进制加法运算，生成密文流

img

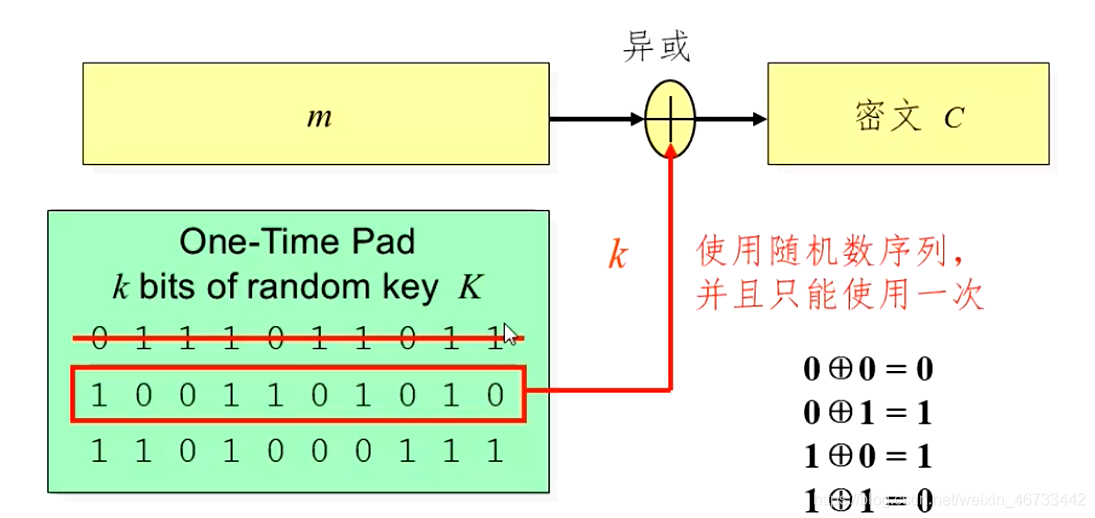
一次一密（one-time pad）

  • 又称Vernam加密法

  • 将明文与随机生成的密钥进行异或运算来实现加密和解密

  • 密钥：与明文等长、完全随机、只使用一次，并且发送者和接收者在事先共享同一密钥。

  • 不能提供完整性验证和认证

    在这里插入图片描述

一次一密的密钥长度和明文一样长，流密码不是，需要种子密钥通过密钥生成器产生密钥流

多次一密（Many Time Pad Attack）

Many-Time-Pad 攻击 (ruanx.net)

多次一密攻击的关键在于密钥重复使用。由于密钥序列在多次加密中重复使用，攻击者可以通过异或运算的性质，推断出密钥流的一部分或全部内容，从而破解密钥和解密密文。

异或运算性质

异或运算的性质交换律                     a⊕b=b⊕a结合律    a⊕b⊕c=a⊕(b⊕c)规定        a⊕a=0      a⊕0=a自反性      a⊕b⊕b=a⊕0=a可移项性  a⊕b=c−>a=b⊕c异或运算的性质\\ 交换律\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ a⊕b=b⊕a\\ 结合律\ \ \ \ a⊕b⊕c=a⊕(b⊕c)\\ 规定 \ \ \ \ \ \ \ \ a⊕a=0\ \ \ \ \ \ a⊕0=a\\ 自反性\ \ \ \ \ \ a⊕b⊕b=a⊕0=a\\ 可移项性\ \ a⊕b = c -> a = b⊕c

这个攻击的原理是 c1⊕c2=(m1⊕key)⊕(m2⊕key)=m1⊕m2c_1⊕c_2 =(m_1⊕key)⊕(m_2⊕key)= m_1⊕m_2，而通过 c1⊕c2c_1⊕c_2 可以分析出 m1⊕m2m_1⊕m_2，因此 m1⊕m2m_1⊕m_2 不再安全。

两个密文的异或，就等于对应明文的异或,可以通过频率分析，来破译这些密文。

ascii表

ascii 码表在 Linux 下可以通过 man ascii 指令查看。它的性质有：

  • 0x20 是空格。 低于 0x20 的，全部是起特殊用途的字符； 0x20~0x7E 的，是可打印字符。
  • 0x30~0x39 是数字 0,1,2...9。
  • 0x41~0x5A 是大写字母 A-Z； 0x61~0x7A 是小写字母 a-z

小写字母 ⊕ 空格，会得到对应的大写字母；大写字母 ⊕ 空格，会得到小写字母！所以，如果x ⊕ y得到一个英文字母，那么中的某一个有很大概率是空格

例题–[AFCTF2018]你听过一次一密么？

题目

25030206463d3d393131555f7f1d061d4052111a19544e2e5d
0f020606150f203f307f5c0a7f24070747130e16545000035d
1203075429152a7020365c167f390f1013170b1006481e1314
0f4610170e1e2235787f7853372c0f065752111b15454e0e09
081543000e1e6f3f3a3348533a270d064a02111a1b5f4e0a18
0909075412132e247436425332281a1c561f04071d520f0b11
4116111b101e2170203011113a69001b475206011552050219
041006064612297020375453342c17545a01451811411a470e
021311114a5b0335207f7c167f22001b44520c15544801125d
06140611460c26243c7f5c167f3d015446010053005907145d
0f05110d160f263f3a7f4210372c03111313090415481d49

攻击击过程显而易见：对于每一条密文c1，拿去异或其他所有密文。然后去数每一列有多少个英文字符，作为c1在这一位是空格的评分。

上面的事情做完时候，依据评分从大到小排序，依次利用 “某个明文的某一位是空格” 这种信息恢复出所有明文的那一列。如果产生冲突，则舍弃掉评分小的。

脚本：

#脚本1
import Crypto.Util.strxor as xo
import libnum, codecs, numpy as np

def isChr(x):
    if ord('a') <= x and x <= ord('z'): return True
    if ord('A') <= x and x <= ord('Z'): return True
    return False


def infer(index, pos):
    if msg[index, pos] != 0:
        return
    msg[index, pos] = ord(' ')
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(' ')

def know(index, pos, ch):
    msg[index, pos] = ord(ch)
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(ch)


dat = []

def getSpace():
    for index, x in enumerate(c):
        res = [xo.strxor(x, y) for y in c if x!=y]
        f = lambda pos: len(list(filter(isChr, [s[pos] for s in res])))
        cnt = [f(pos) for pos in range(len(x))]
        for pos in range(len(x)):
            dat.append((f(pos), index, pos))

c = [codecs.decode(x.strip().encode(), 'hex') for x in open('Problem.txt', 'r').readlines()]

msg = np.zeros([len(c), len(c[0])], dtype=int)

getSpace()

dat = sorted(dat)[::-1]
for w, index, pos in dat:
    infer(index, pos)

know(10, 21, 'y')
know(8, 14, 'n')

print('\n'.join([''.join([chr(c) for c in x]) for x in msg]))

key = xo.strxor(c[0], ''.join([chr(c) for c in msg[0]]).encode())
print(key)
#脚本2
#!/usr/bin/python
## OTP - Recovering the private key from a set of messages that were encrypted w/ the same private key (Many time pad attack) - crypto100-many_time_secret @ alexctf 2017
# Original code by jwomers: https://github.com/Jwomers/many-time-pad-attack/blob/master/attack.py)

import string
import collections
import sets, sys

# 11 unknown ciphertexts (in hex format), all encrpyted with the same key
c1='daaa4b4e8c996dc786889cd63bc4df4d1e7dc6f3f0b7a0b61ad48811f6f7c9bfabd7083c53ba54'
c2='c5a342468c8c7a88999a9dd623c0cc4b0f7c829acaf8f3ac13c78300b3b1c7a3ef8e193840bb'
c3='dda342458c897a8285df879e3285ce511e7c8d9afff9b7ff15de8a16b394c7bdab920e7946a05e9941d8308e'
c4='d9b05b4cd5ce7c8f938bd39e24d0df191d7694dfeaf8bfbb56e28900e1b8dff1bb985c2d5aa154'
c5='d9aa4b00c88b7fc79d99d38223c08d54146b88d3f0f0f38c03df8d52f0bfc1bda3d7133712a55e9948c32c8a'
c6='c4b60e46c9827cc79e9698936bd1c55c5b6e87c8f0febdb856fe8052e4bfc9a5efbe5c3f57ad4b9944de34'
c7='d9aa5700da817f94d29e81936bc4c1555b7b94d5f5f2bdff37df8252ffbecfb9bbd7152a12bc4fc00ad7229090'
c8='c4e24645cd9c28939a86d3982ac8c819086989d1fbf9f39e18d5c601fbb6dab4ef9e12795bbc549959d9229090'
c9='d9aa4b598c80698a97df879e2ec08d5b1e7f89c8fbb7beba56f0c619fdb2c4bdef8313795fa149dc0ad4228f'
c10='cce25d48d98a6c8280df909926c0de19143983c8befab6ff21d99f52e4b2daa5ef83143647e854d60ad5269c87'
c11='d9aa4b598c85668885df9d993f85e419107783cdbee3bbba1391b11afcf7c3bfaa805c2d5aad42995ede2cdd82977244'
ciphers = [c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11]
# The target ciphertext we want to crack

# XORs two string
def strxor(a, b):     # xor two strings (trims the longer input)
    return "".join([chr(ord(x) ^ ord(y)) for (x, y) in zip(a, b)])

def target_fix(target_cipher):
    print '-------begin-------'

    # To store the final key
    final_key = [None]*150
    # To store the positions we know are broken
    known_key_positions = set()

    # For each ciphertext
    for current_index, ciphertext in enumerate(ciphers):
        counter = collections.Counter()
        # for each other ciphertext
        for index, ciphertext2 in enumerate(ciphers):
            if current_index != index: # don't xor a ciphertext with itself
                for indexOfChar, char in enumerate(strxor(ciphertext.decode('hex'), ciphertext2.decode('hex'))): # Xor the two ciphertexts
                    # If a character in the xored result is a alphanumeric character, it means there was probably a space character in one of the plaintexts (we don't know which one)
                    if char in string.printable and char.isalpha(): counter[indexOfChar] += 1 # Increment the counter at this index
        knownSpaceIndexes = []

        # Loop through all positions where a space character was possible in the current_index cipher
        for ind, val in counter.items():
            # If a space was found at least 7 times at this index out of the 9 possible XORS, then the space character was likely from the current_index cipher!
            if val >= 7: knownSpaceIndexes.append(ind)
        #print knownSpaceIndexes # Shows all the positions where we now know the key!

        # Now Xor the current_index with spaces, and at the knownSpaceIndexes positions we get the key back!
        xor_with_spaces = strxor(ciphertext.decode('hex'),' '*150)
        for index in knownSpaceIndexes:
            # Store the key's value at the correct position
            final_key[index] = xor_with_spaces[index].encode('hex')
            # Record that we known the key at this position
            known_key_positions.add(index)

    # Construct a hex key from the currently known key, adding in '00' hex chars where we do not know (to make a complete hex string)
    final_key_hex = ''.join([val if val is not None else '00' for val in final_key])
    # Xor the currently known key with the target cipher
    output = strxor(target_cipher.decode('hex'),final_key_hex.decode('hex'))

    print "Fix this sentence:"
    print ''.join([char if index in known_key_positions else '*' for index, char in enumerate(output)])+"\n"

    # WAIT.. MANUAL STEP HERE 
    # This output are printing a * if that character is not known yet
    # fix the missing characters like this: "Let*M**k*ow if *o{*a" = "cure, Let Me know if you a"
    # if is too hard, change the target_cipher to another one and try again
    # and we have our key to fix the entire text!

    #sys.exit(0) #comment and continue if u got a good key

    print '------end------'
    
for i in ciphers:
    target_fix(i)

伪随机密钥流

伪随机序列

伪随机序列也就是，即使截获其中一段,也无法推测后面是什么。（只能要求截获比周期短的一段密钥流时不会泄露更多信息, 这样的序列称为伪随机序列。）

伪随机数生成器

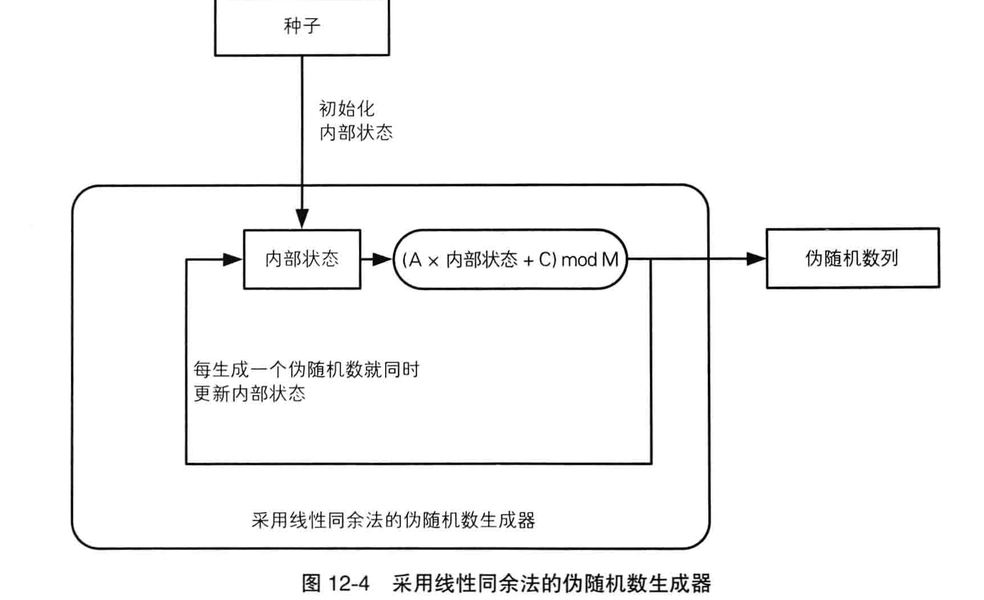
线性同余生成器 / 线性同余方法（LCG）

线性同余方法（LCG）是个产生伪随机数的方法

《图解密码技术》笔记（二） | yucs's Blog

LCG的性能和随机性取决于选取的参数。如果选择恰当的参数，LCG可以生成长周期和均匀分布的伪随机数序列。然而，不恰当的参数选择可能导致序列的周期较短或者存在可预测的模式，从而影响其随机性和安全性

LCG的周期最大为 MM，但大部分情况都会少于 MM。要令LCG达到最大周期，应符合以下条件：

  1. B,MB,M 互质；
  2. MM 的所有质因数都能整除 A−1A-1；
  3. 若 MM 是4的倍数，A−1A-1 也是；
  4. A,B,N0A,B,N_{0} 都比 MM 小；
  5. A,BA,B 是正整数。
from functools import reduce
from math import gcd
from Crypto.Util.number import *

def egcd(a, b):
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = egcd(b % a, a)
        return (g, x - (b // a) * y, y)

def modinv(a, m):
    g, x, y = egcd(a, m)
    if g != 1:
        raise Exception('modular inverse does not exist')
    else:
        return x % m

def crack_unknown_increment(states, modulus, multiplier):
    increment = (states[1] - states[0]*multiplier) % modulus
    return modulus, multiplier, increment

def crack_unknown_multiplier(states, modulus):
    multiplier = (states[2] - states[1]) * modinv(states[1] - states[0], modulus) % modulus
    return crack_unknown_increment(states, modulus, multiplier)

def crack_unknown_modulus(states):
    diffs = [s1 - s0 for s0, s1 in zip(states, states[1:])]
    zeroes = [t2*t0 - t1*t1 for t0, t1, t2 in zip(diffs, diffs[1:], diffs[2:])]
    modulus = abs(reduce(gcd, zeroes))
    return crack_unknown_multiplier(states, modulus)

# N[i+1] = (A*N[i]+B) % M
# A,B,N均未知
sequence = []
modulus, multiplier, increment = crack_unknown_modulus(sequence)
print('A = '+str(multiplier))
print('B = '+str(increment))
print('N = '+str(modulus))

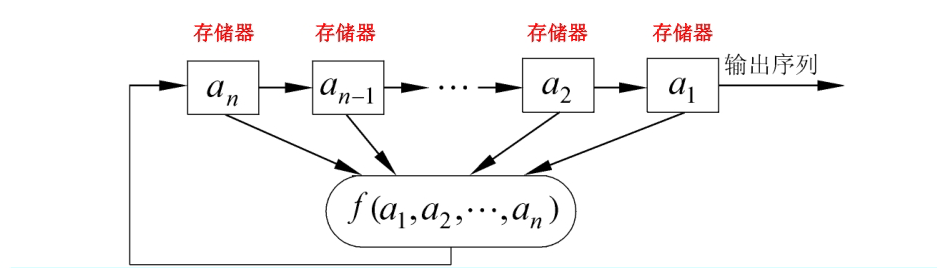
线性反馈移位寄存器（Linear Feedback Shift Register，简称LFSR）

用于生成一个伪随机的比特序列，常用于加密、编码、通信等领域。

移位寄存器是流密码产生密钥流的一个主要组成部分，GF（2）上一个n级反馈移位寄存器由n个二元存储器与一个反馈函数组成。

img

移位寄存器三要素：

  1. 初始状态：由用户确定
  2. 反馈函数：f(a1,a2,⋯ ,an)f(a_1,a_2,\cdots,a_n) 是 nn 元布尔函数，即函数的自变量和因变量只取0和1这两个可能值（题目给出）
  3. 输出序列

image-20230715153526370

对于 nn 级线性反馈移位寄存器

  • 最长周期为 2n−12^n-1（排除全0），达到最长周期的序列一般称为 mm 序列。
  • 完全由其反馈函数决定。
  • n级LFSR状态数：最多有2^n个
  • 输出序列的周期 = 状态周期 <= 2^n - 1

MT19937（梅森旋转算法（Mersenne Twister Algorithm，简称 MT））

​ 为了解决过去伪随机数发生器（Pseudo-Random Number Generator，简称 PRNG）产生的伪随机数质量不高而提出的新算法。常见的两种为基于32位的 MT19937和基于64位的 MT19937-64。

由于梅森旋转算法是利用**线性反馈移位寄存器（LFSR）**产生随机数的，对于LFRS有结论：一个 k 位的移位寄存器，选取合适的特征多项式（即加1为本原多项式）时，取得最大周期 2k−12^k-1.

而MT19937梅森旋转算法的周期为$ 2^{19937}−1$ （正如算法名，这是一个梅森素数），说明它是一个19937级的线性反馈移位寄存器，梅森旋转算法是利用线性反馈寄存器一直进行移位旋转，因此实际上 MT19937-32只需要用32位就能做到。它能做到在 $1≤k≤623 $都可以均匀分布。

Mersenne Twister 最常见的实现方式使用 624 个 32 bits 的初始状态。这些整数按顺序分发（分发前对每个初始数进行转换），分发完后对该状态应用某种算法以获取下一组 624 个整数。以及可以通过得到连续的 624 个输出，还原出原来的 624 个 states，再根据原算法推算出接下来每个 state 下一次的 value，从而算出接下来的输出

算法

整个算法主要分为三个阶段：

  • 第一阶段：获得基础的梅森旋转链；

  • 第二阶段：对于旋转链进行旋转算法；

  • 第三阶段：对于旋转算法所得的结果进行处理；

第一阶段

导入seed，初始化伪随机数发生器

使用一个循环从索引1到623的范围，为 mt 列表的其他元素赋值。赋值的方式基于 Mersenne Twister 算法的核心公式。

  • _int32() 是一个辅助函数，用于确保结果是32位有符号整数。
  • (self.mt[i - 1] ^ self.mt[i - 1] >> 30) 表示对 mt 列表中前一个元素进行右移30位的操作，然后与前一个元素进行异或运算。
  • 1812433253 是一个常数。
  • + i 表示将索引值加到结果中，以产生不同的种子序列。
第二阶段

进行 twist() 函数

==twist() 方法==用于对生成器的状态进行旋转操作。它的操作步骤如下：

  1. 使用一个循环从索引0到623的范围，依次处理每个状态元素。
  2. 根据状态元素的索引，获取当前元素和下一个元素的值。
  3. 对获取的值进行位操作，包括按位与和按位异或，以改变当前元素的值。（
  4. (self.mt[i] & 0x80000000) 获取当前元素的最高位，(self.mt[(i + 1) % 624] & 0x7fffffff) 获取下一个元素的其余31位。这样可以将当前元素的最高位和下一个元素的其余31位合并成一个32位的值。将获取的值存储到变量 y 中，并使用 _int32() 函数将其转换为32位有符号整数。对当前元素进行状态扭曲操作。首先，使用右移运算符将 y 的值向右移动1位，然后与索引为 (i + 397) % 624 的状态元素进行按位异或运算。如果 y 的值除以2的余数不为0，即 y % 2 != 0，则将当前元素与常数 0x9908b0df 进行按位异或运算。）
  5. 将结果存储回 mt 列表的当前元素位置。
第三阶段

==extract_number() 方法==用于从生成器中提取一个伪随机数。它的操作步骤如下：

  1. 首先，检查 mti（mti 是用于追踪 mt 列表中当前使用的元素的索引) 是否等于0，如果等于0，则调用 twist() 方法进行状态的扭曲操作，以生成新的伪随机数序列。
  2. 接下来，从 mt 列表中获取当前的随机数，存储到变量 y 中。
  3. 对 y 执行一系列的位运算操作，包括右移、异或、左移和按位与，以改变 y 的值。
  4. 更新 mti 的值，将其加1并对624取模，以确保它在0到623之间循环。
  5. 返回 _int32(y)，其中 _int32() 是一个辅助函数，用于确保结果是32位有符号整数。

实现

使用MT19937算法生成范围在 [232−1]
的均匀分布的32位整数。

def _int32(x):
    return int(0xFFFFFFFF & x)
  
class MT19937:
    # 用于初始化伪随机数生成器的类的构造函数
    # 根据seed初始化624的state
    def __init__(self, seed):
   #创建一个名为 mt 的列表，包含624个元素，初始值都为0。这是用于存储生成器状态的主要数据结构。
        self.mt = [0] * 624
   #将输入参数 seed 的值赋给 mt 列表的第一个元素。它用于初始化生成器的种子。
        self.mt[0] = seed
   #mti 是用于追踪 mt 列表中当前使用的元素的索引。
        self.mti = 0
        for i in range(1, 624):
            self.mt[i] = _int32(1812433253 * (self.mt[i - 1] ^ self.mt[i - 1] >> 30) + i)
  
    # 提取伪随机数
    def extract_number(self):
        if self.mti == 0:
            self.twist()
        y = self.mt[self.mti]
        y = y ^ y >> 11
        y = y ^ y << 7 & 2636928640
        y = y ^ y << 15 & 4022730752
        y = y ^ y >> 18
        self.mti = (self.mti + 1) % 624
        return _int32(y)
  
    # 对状态进行旋转
    def twist(self):
        for i in range(0, 624):
            y = _int32((self.mt[i] & 0x80000000) + (self.mt[(i + 1) % 624] & 0x7fffffff))
            self.mt[i] = (y >> 1) ^ self.mt[(i + 397) % 624]
            if y % 2 != 0:
                self.mt[i] = self.mt[i] ^ 0x9908b0df

破解

Mersenne Twister 梅森旋转算法笔记 | 独奏の小屋 (hasegawaazusa.github.io)

右移位后异或逆向
def unshiftRight(self, x, shift):
    res = x
    for i in range(32):
        res = x ^ res >> shift
    return res
左移位后异或逆向
def unshiftLeft(self, x, shift, mask):
    res = x
    for i in range(32):
        res = x ^ (res << shift & mask)
    return res
提取伪随机数逆向
b = 0x9d2c5680
c = 0xefc60000
def untemper(self, v):
    v = self.unshiftRight(v, 18)
    v = self.unshiftLeft(v, 15, self.c)
    v = self.unshiftLeft(v, 7, self.b)
    v = self.unshiftRight(v, 11)
    return v
通过输出参数逆向
# forward 表示是否需要回到目前状态
def go(self, outputs, forward=True):
    # 还原的寄存器状态
    result_state = None

    # 至少需要 624 个寄存器状态
    assert len(outputs) >= 624

    ivals = []
    for i in range(624):
        ivals.append(self.untemper(outputs[i]))

    if len(outputs) >= 625:
        # 此时可以使用后面的数据进行验证
        challenge = outputs[624]
        for i in range(1, 626):
            state = (3, tuple(ivals+[i]), None)
            r = random.Random()
            r.setstate(state)

            if challenge == r.getrandbits(32):
                result_state = state
                break
    else:
        # 如果刚好是 624 个寄存器状态
        result_state = (3, tuple(ivals+[624]), None)

    # 利用 python 自带的 mt19937 random 库
    rand = random.Random()
    rand.setstate(result_state)

    # 如果需要到输出后的状态，则进行比较判断
    if forward:
        for i in range(624, len(outputs)):
            assert rand.getrandbits(32) == outputs[i]

    return rand
完整代码
class MT19937Recover:
    def unshiftRight(self, x, shift):
        res = x
        for i in range(32):
            res = x ^ res >> shift
        return res

    def unshiftLeft(self, x, shift, mask):
        res = x
        for i in range(32):
            res = x ^ (res << shift & mask)
        return res

    def untemper(self, v):
        v = self.unshiftRight(v, 18)
        v = self.unshiftLeft(v, 15, 0xefc60000)
        v = self.unshiftLeft(v, 7, 0x9d2c5680)
        v = self.unshiftRight(v, 11)
        return v

    def go(self, outputs, forward=True):
        result_state = None

        assert len(outputs) >= 624

        ivals = []
        for i in range(624):
            ivals.append(self.untemper(outputs[i]))

        if len(outputs) >= 625:
            challenge = outputs[624]
            for i in range(1, 626):
                state = (3, tuple(ivals+[i]), None)
                r = random.Random()
                r.setstate(state)

                if challenge == r.getrandbits(32):
                    result_state = state
                    break
        else:
            result_state = (3, tuple(ivals+[624]), None)

        rand = random.Random()
        rand.setstate(result_state)

        if forward:
            for i in range(624, len(outputs)):
                assert rand.getrandbits(32) == outputs[i]

        return rand

mtc = MT19937Recover()

流密码的分类

依据流密码密钥序列产生的方式，可以将流密码分为同步流密码和自同步流密码两类。

同步流密码：如果密钥流产生的算法和产生的密钥序列都与明文或密文无关，我们称这类流密码为同步流密码。

自同步流密码：密钥流产生的算法与明文相关，则所产生的密钥序列也与明文相关，称这类流密码为自同步流密码

同步流密码

同步流密码可以分为密钥流产生器和加密变换器两部分

在同步流密码中，前面出现的加解密错误不会影响到后面的加解密，这是因为相邻两位明文的加密是相互独立，没有关系的。

同步流密码在加密或解密时，需要使两者密钥流生成器的状态一致（这里的状态可以决定密钥流生成器产生的密钥），否则会导致加解密密钥不一致，使解密失败。当两者密钥流生成器的状态不一致时，必须借助外接手段来同步，同步流密码本身不具有自同步功能，FB、CTR模式就属于同步流密码

自同步流密码

密钥产生算法是密钥和以往密文序列的函数，则称这种流密码为自同步流密码。

自同步流密码中，密钥序列的产生与明文的加密是不独立的，也是不能分割的。很多情况下，明文或者密文都需要给密钥序列的产生提供反馈。

自同步流密码具有自同步功能。因为密钥序列的产生与明密文序列有关，所以加密和解密密钥生成器的状态不一致时，是可以自己进行同步的，无需认为同步。

自同步流密码可能会对错误进行传播。因为密钥序列的产生与明文序列有关，所以前边明文的加密错误，会导致后边密钥序列生成出错，导致后边明文序列也加密错误。

CFB模式就属于同步流密码

常见流密码

RC4

  • RC4由伪随机数生成器和异或运算组成。
  • RC4的密钥长度可变，范围是[1,255]。
  • RC4一个字节一个字节地加解密。
  • 给定一个密钥，伪随机数生成器接受密钥并产生一个S盒。S盒用来加密数据，而且在加密过程中S盒会变化。
  • 由于异或运算的对合性，RC4加密解密使用同一套算法。

RC4产生非线性的密钥流序列，先密钥调度算法初始化S表，再伪随机生成算法修改S表选取随机元素作为k
密钥调度算法

  1. 对S表线性填充，S(0)=0,S(1)=1,⋯ \cdots⋯,S(255)=255. S盒（0-255）

  2. 种子密钥重复填充K表，K(0)=1,K(1)=2,K(3)=3,K(4)=1,K(5)=2,⋯ ⋯( K 表只有（1，模)）

  3. #密钥调度算法
int j=0
for i in range(256):

    
  	j=j+S(i)+K(i)(mod256)
  	t=S(i)
  	  #/交换S(i)、S(j)、swap(S(i),S(j));
  	S(i)=S(j)
  	S(j)=t

  #伪随机生成算法
  i=0,j=0
  i=i+1(mod256)
  j=j+S(i)(mod256)
  #交换S(i)、S(j)
  t=S(i)+S(j)(mod256)
  #输出密钥字
  k=S(t)

  

  ```python
  伪随机生成算法
4. i=0,j=0
5. i=i+1(mod256)
6. j=j+S(i)(mod256)
7. 交换S(i)、S(j)
8. t=S(i)+S(j)(mod256)
9. 输出密钥字k=S(t)