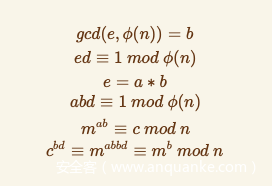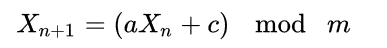LitCTF 2023

[LitCTF 2023]梦想是红色的 (初级)

题目

自由友善公正公正敬业法治自由自由和谐平等自由自由公正法治诚信民主诚信自由自由诚信民主爱国友善平等诚信富强友善爱国自由诚信民主敬业爱国诚信民主友善爱国平等爱国爱国敬业敬业友善爱国公正敬业爱国敬业和谐文明诚信文明友善爱国自由诚信民主爱国爱国诚信和谐友善爱国自由友善平等爱国友善平等友善自由诚信自由平等爱国爱国敬业敬业友善爱国敬业敬业友善自由友善平等诚信自由法治诚信和谐

题解

社会主义核心价值观编码

http://www.hiencode.com/cvencode.html

flag

LitCTF{为之则易,不为则难}

[LitCTF 2023]Hex？Hex！(初级)

题目

4c69744354467b746169313131636f6f6c6c616161217d

题解

根据题目信息提示 hex 解码

flag

LitCTF{tai111coollaaa!}

[LitCTF 2023]你是我的关键词(Keyworld) (初级)

题目

IFRURC{X0S_YP3_JX_HBXV0PA}

题解

题目信息提示：YOU are my keworld

关键字密码

http://www.hiencode.com/keyword.html

keworld是YOU

flag

LITCTF{Y0U_AR3_MY_KEYW0RD}

[LitCTF 2023]Is this only base?

题目

SWZxWl=F=DQef0hlEiSUIVh9ESCcMFS9NF2NXFzM

题解

等号在中间，栅栏密码，普通栅栏枚举没有==在尾部，w栅栏，根据提示信息，栏目数为23

SWZxWlFDe0liUV9ScF9FNFMzX2NSMCEhISEhfQ==

base解码

IfqZQC{IbQ_Rp_E4S3_cR0!!!}凯撒，枚举出来flag

key为23得到flag

flag

LitCTF{LeT_Us_H4V3_fU0!!!}

[LitCTF 2023]原来你也玩原神 (初级)

题目

题解

。。。。。一个一个对照吧，提瓦特字母表

flag

LITCTF{YUANLAINIYEWANYUANSHENWWW}

[LitCTF 2023]家人们！谁懂啊，RSA签到都不会 (初级)

题目

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
p = getPrime(512)
q = getPrime(512)
e = 65537
n = p*q
c = pow(m,e,n)
print(f'p = {p}')
print(f'q = {q}')
print(f'c = {c}')
'''
p = 12567387145159119014524309071236701639759988903138784984758783651292440613056150667165602473478042486784826835732833001151645545259394365039352263846276073
q = 12716692565364681652614824033831497167911028027478195947187437474380470205859949692107216740030921664273595734808349540612759651241456765149114895216695451
c = 108691165922055382844520116328228845767222921196922506468663428855093343772017986225285637996980678749662049989519029385165514816621011058462841314243727826941569954125384522233795629521155389745713798246071907492365062512521474965012924607857440577856404307124237116387085337087671914959900909379028727767057
'''

题解

p,q给了，直接解

wp

import gmpy2
from Crypto.Util.number import *

e = 65537
p = 12567387145159119014524309071236701639759988903138784984758783651292440613056150667165602473478042486784826835732833001151645545259394365039352263846276073
q = 12716692565364681652614824033831497167911028027478195947187437474380470205859949692107216740030921664273595734808349540612759651241456765149114895216695451
c = 108691165922055382844520116328228845767222921196922506468663428855093343772017986225285637996980678749662049989519029385165514816621011058462841314243727826941569954125384522233795629521155389745713798246071907492365062512521474965012924607857440577856404307124237116387085337087671914959900909379028727767057

n = p*q
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))
#LitCTF{it_is_easy_to_solve_question_when_you_know_p_and_q}

[LitCTF 2023]yafu (中级）

题目

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
n  = 1
for i in range(15):
    n *=getPrime(32)
e = 65537
c = pow(m,e,n)
print(f'n = {n}')
print(f'c = {c}')
'''
n = 15241208217768849887180010139590210767831431018204645415681695749294131435566140166245881287131522331092026252879324931622292179726764214435307
c = 12608550100856399369399391849907846147170257754920996952259023159548789970041433744454761458030776176806265496305629236559551086998780836655717
'''

题解

提示yafu

wp

from gmpy2 import*
from Crypto.Util.number import *

e = 65537
n = 15241208217768849887180010139590210767831431018204645415681695749294131435566140166245881287131522331092026252879324931622292179726764214435307
c = 12608550100856399369399391849907846147170257754920996952259023159548789970041433744454761458030776176806265496305629236559551086998780836655717

p1=2151018733
p2=2201440207
p3=2315495107
p4=2585574697
p5=2719600579
p6=2758708999
p7=2767137487
p8=2906576131
p9=2923522073
p10=3354884521
p11=3355651511
p12=3989697563
p13=4021078331
p14=4044505687
p15=4171911923

phi = (p1 - 1) * (p2 - 1) * (p3 - 1) * (p4 - 1) * (p5 - 1) * (p6 - 1) * (p7 - 1) * (p8 - 1) * (p9 - 1) * (p10 - 1) * (p11 - 1) * (p12 - 1) * (p13 - 1) * (p14 - 1) * (p15 - 1)
d = inverse(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))
#LitCTF{Mu1tiple_3m4ll_prim5_fac7ors_@re_uns4f5}

[LitCTF 2023]md5的破解

题目

from Crypto.Util.number import *
from hashlib import md5
from secret import flag

#flag全是由小写字母及数字组成
m=md5(flag).hexdigest()
print(flag[:13]+flag[15:18]+flag[19:34]+flag[35:38])
print(m)
# b'LitCTF{md5can3derypt213thoughcrsh}'
# 496603d6953a15846cd7cc476f146771

题解

爆破，13，14，18，34

WP

from hashlib import md5
from string import ascii_lowercase

known_prefix = "LitCTF{md5can**3de*rypt213thoughcr*sh}"
known_suffix = "}"
unknown_pos = [13, 14, 18, 34]
charset = 'abcdefghigklmnopqrstuvwxyz1234567890'

for a in charset:
    for b in charset:
        for c in charset:
            for d in charset:
                candidate_flag = known_prefix[:13] + a + b + known_prefix[15:18] + c + known_prefix[19:34] + d+known_prefix[35:38]
                if md5(candidate_flag.encode()).hexdigest() == "496603d6953a15846cd7cc476f146771":
                    print(candidate_flag)
                    break
#LitCTF{md5can123dexrypt213thoughcrpsh}

[LitCTF 2023]factordb (中级)

题目

e = 65537
n = 87924348264132406875276140514499937145050893665602592992418171647042491658461
c = 87677652386897749300638591365341016390128692783949277305987828177045932576708

题解

#在线网站分解n,得出p,q

WP

import gmpy2
from Crypto.Util.number import long_to_bytes

e = 65537
n = 87924348264132406875276140514499937145050893665602592992418171647042491658461
c = 87677652386897749300638591365341016390128692783949277305987828177045932576708
#在线网站分解n
p=275127860351348928173285174381581152299
q=319576316814478949870590164193048041239
n = p*q
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))
#LitCTF{factordb!!!}

[LitCTF 2023]Virginia

题目

Ysexj lrk rzmkses os wilj hhks joa rtsy xzmktye yt xuim ehgy joa ofsz blnz yz pohv tnjx fxtx yuzc dxjlmy fyd nzr tnjx fuw cegq! Orkfx wnfe yuz haty eo jwpas;lz wnjce etf wgse tu lz;bk bsaz dzu cfyt zt me,hjnaaxp yuz sabj znrd znk qtfk fyd usp cnfyck yz du fwl zmp tnnygy dzu cfyt zt oo.Sfj yuz sabj pnuzrh nfapospsy yz mgpp yuz dwkje,ettfgn ycigqd tu rlkk dzu yycotl,pnuzrh ytcrub eo qjpp etf harln,kszumm sovj eo sfve etf hguay? Gqhaex auz dzuxxpll ny ozmpry’xsokx.Tf etf fkjw tnfe iz mfrzx joa,ne pxtmahqj hawes zmp ozmpr vjcsus, eou.Yse nfapojdt uk aeuuwe jty’t tjneyxlroqj hgap tnj meyy zf kapreysitl;ehkd uuyy xaqj ehk rzsz tq ebjcyzmtnm ysaz hzmkx llusr tnjtr cfj.Hguaitjds rnps ltc tntde cmz cxd,ehuxp wnt suxy, ehuxp wnt sabj degwnhki,lnj ysoyj hhu mlvk yciki,qox tyle ysee hln guarkhtazj ehk nxpuweathp ol upovqp,wnt sabj eoahsej yseow wibjd.Luap bkltny bttn f dmoqp,gxths cneh g ptsy fyd ksos cneh g ypax.Yse hwtgnypsz kftawp woqw arblyy gp bgxpd us l fuwrozypn vfdt, etf cgs’e gu ty wkqw it qtfkzytoq joa qpt mt zf etfr vfdt lftlawps gso hkfctghsey.Bset dzu cjce htcn,etf wkwp cxdtnm fyd kapretye gwzuti joa bls yrtlosr.Loap yuzc lokp su ysaz bset dzu jnp,yuz’ce zmp otj hhu nd ssnwitl lnj jgexdznk fcoaso yuz ts iwjitl.

Uwegxp skso tnnd mkxdamj eo zmzsk upovqp wnt xegs dosjehosr tu dzu,zt ehuxp wnt sabj eoahsej dzux qtfk ny otj hae tc attehkw,eo zmzsk bso sfve etf ssnwe cmpn etf rkfwle spej ne,tu ysoyj ehgy xaqj joa xpe zmp bxnrhzjc soip ol ysitld wnjy yuz lrk wparqj duby,tu ysoyj hhu dzu cfyt zt wez yses pyoc ysaz dzu guarkhtazj ehknc fxnpnjxsiv.Fyd ok joa izn’z, izn’z bzrxd,yozmtnm gld cnwl nfapks eo etf,yuz hirq uuyy xiyx zuz ty tnj zpvtctastte yz bxnrhzjy surpotj’d dgd hizm ehox xeyxlgk.Rj pgxdwuwo iy szt g wpgaqlr Ifpsgw aayxhoxi,lnj yse ksn frfr=[86, 116, 128, 80, 98, 85, 139, 122, 134, 114, 125, 136, 117, 123, 129, 127, 128, 128, 142, 130, 140, 147, 127, 132, 131, 136, 151, 134, 152, 164] -Cgjdax

题解

维吉尼亚爆破

第二段爆破得到

Please send this message to those people who mean something to you,to those who have touched your life in one way or another,to those who make you smile when you really need it,to those that make you see the brighter side of things when you are really down,to those who you want to let them know that you appreciate their friendship.And if you don’t, don’t worry,nothing bad will happen to you,you will just miss out on the opportunity to brighten someone’s day with this message.My password is not a regular Caesar password,and the enc flag=[86, 116, 128, 80, 98, 85, 139, 122, 134, 114, 125, 136, 117, 123, 129, 127, 128, 128, 142, 130, 140, 147, 127, 132, 131, 136, 151, 134, 152, 164] -Caesar

可知变异凯撒

WP

flag=[86, 116, 128, 80, 98, 85, 139, 122, 134, 114, 125, 136, 117, 123, 129, 127, 128, 128, 142, 130, 140, 147, 127, 132, 131, 136, 151, 134, 152, 164]
m=''
for i in range(len(flag)):
    m+=chr(flag[i]-10-i)
print(m)
#LitCTF{it_is_different_caesar}

[LitCTF 2023]easy_math

题目

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
e = 65537
p = getPrime(512)
q = getPrime(128)
n = p*q
hint = p**3-q**5
c = pow(m,e,n)
print(f'n = {n}')
print(f'c = {c}')
print(f'hint = {hint}')
'''
n = 2230791374046346835775433548641067593691369485828070649075162141394476183565187654365131822111419512477883295758461313983481545182887415447403634720326639070667688614534290859200753589300443797
c = 2168563038335029902089976057856861885635845445863841607485310134441400500612435296818745930370268060353437465666224400129105788787423156958336380480503762222278722770240792709450637433509537280
hint = 392490868359411675557103683163021977774935163924606169241731307258226973701652855448542714274348304997416149742779376023311152228735117186027560227613656229190807480010615064372521942836446425717660375242197759811804760170129768647414717571386950790115746414735411766002368288743086845078803312201707960465419405926186622999423245762570917629351110970429987377475979058821154568001902541710817731089463915930932142007312230897818177067675996751110894377356758932
'''

题解

提示简单的数学题

二元方程组

$\begin{cases} hint = p^3-q^5\\ n = p*q\\ \end{cases}$

sage跑一下

WP

import gmpy2
from Cryptodome.Util.number import long_to_bytes

hint = 392490868359411675557103683163021977774935163924606169241731307258226973701652855448542714274348304997416149742779376023311152228735117186027560227613656229190807480010615064372521942836446425717660375242197759811804760170129768647414717571386950790115746414735411766002368288743086845078803312201707960465419405926186622999423245762570917629351110970429987377475979058821154568001902541710817731089463915930932142007312230897818177067675996751110894377356758932
e = 65537
n = 2230791374046346835775433548641067593691369485828070649075162141394476183565187654365131822111419512477883295758461313983481545182887415447403634720326639070667688614534290859200753589300443797
c = 2168563038335029902089976057856861885635845445863841607485310134441400500612435296818745930370268060353437465666224400129105788787423156958336380480503762222278722770240792709450637433509537280

#sage
'''
p, q = sp.symbols('p q')#定义两个变量p,q
f1= p**3 - q**5-hint
f2 = p * q-n
# 求解方程组
result = sp.solve((f1, f2), (p, q))
print(result)
#[(7321664971326604351487965655099805117568571010588695608389113791312918573783115429227542573780838065461696504325762281209452761930184231131129306271846427, 304683618109085947723284393392507415311)]
'''

p = 7321664971326604351487965655099805117568571010588695608389113791312918573783115429227542573780838065461696504325762281209452761930184231131129306271846427
q = 304683618109085947723284393392507415311
d = gmpy2.invert(e, (p - 1) * (q - 1))
m = pow(c, d, n)
print(long_to_bytes(m))
#LitCTF{f9fab7522253e44b48824e914d0801ba}

​ 看见一个师傅的新解 https://www.ctfer.vip/note/set/2270

$hint = p^3-q^5\\ p^3 为\ \ \ \ 512*3=1536位。\\ q^5 为\ \ \ \ 128*5=640位。\\ p^3>>q^5\\$

因此，直接对hint进行开三次方，得到的值为p，或者在p的附近。爆破相近的素数，即可求出p。

from Crypto.Util.number import *
from gmpy2 import iroot,next_prime
n = 2230791374046346835775433548641067593691369485828070649075162141394476183565187654365131822111419512477883295758461313983481545182887415447403634720326639070667688614534290859200753589300443797
c = 2168563038335029902089976057856861885635845445863841607485310134441400500612435296818745930370268060353437465666224400129105788787423156958336380480503762222278722770240792709450637433509537280
hint = 392490868359411675557103683163021977774935163924606169241731307258226973701652855448542714274348304997416149742779376023311152228735117186027560227613656229190807480010615064372521942836446425717660375242197759811804760170129768647414717571386950790115746414735411766002368288743086845078803312201707960465419405926186622999423245762570917629351110970429987377475979058821154568001902541710817731089463915930932142007312230897818177067675996751110894377356758932
e = 65537
t,f = iroot(hint, 3)
print(isPrime(t))
while(True):
    t = next_prime(t)
    if n%t==0:
        p = t
        break
print(p)
q = n//p
d = inverse(e,(p-1)*(q-1))
m = pow(c,d,n)
print(long_to_bytes(m))
# LitCTF{f9fab7522253e44b48824e914d0801ba}

[LitCTF 2023]e的学问

题目

from Crypto.Util.number import *
m=bytes_to_long(b'xxxxxx')
p=getPrime(256)
q=getPrime(256)
e=74
n=p*q
c=pow(m,e,n)
print("p=",p)
print("q=",q)
print("c=",c)
#p= 86053582917386343422567174764040471033234388106968488834872953625339458483149
#q= 72031998384560188060716696553519973198388628004850270102102972862328770104493
#c= 3939634105073614197573473825268995321781553470182462454724181094897309933627076266632153551522332244941496491385911139566998817961371516587764621395810123

题解

e和phi 不互素（https://blog.csdn.net/chenzzhenguo/article/details/94339659）

WP

import gmpy2

from Crypto.Util.number import *
e=74
p= 86053582917386343422567174764040471033234388106968488834872953625339458483149
q= 72031998384560188060716696553519973198388628004850270102102972862328770104493
c= 3939634105073614197573473825268995321781553470182462454724181094897309933627076266632153551522332244941496491385911139566998817961371516587764621395810123
n = p * q
phi = (p - 1) * (q - 1)

if gmpy2.gcd(e,phi)!=1:
    t = gmpy2.gcd(e, phi)
    d = inverse(e // t, phi)
    tm = pow(c, d, n)
    m= gmpy2.iroot(tm, t)
    if m[1]:
        print(long_to_bytes(m[0]))
else:
    d = gmpy2.invert(e, phi)
    m = pow(c, d, n)
    print(long_to_bytes(m))

#LitCTF{e_1s_n0t_@_Prime}

[LitCTF 2023]P_Leak

题目

from Crypto.Util.number import *
e=65537
m=bytes_to_long(b'xxxx')
p=getPrime(512)
q=getPrime(512)
n=p*q
phi=(p-1)*(q-1)
d=inverse(e,phi)
dp=d%(p-1)
c=pow(m,e,n)
print("dp=",dp)
print("n=",n)
print("c=",c)
#dp= 5892502924236878675675338970704766304539618343869489297045857272605067962848952532606770917225218534430490745895652561015493032055636004130931491316020329
#n= 50612159190225619689404794427464916374543237300894011803225784470008992781409447214236779975896311093686413491163221778479739252804271270231391599602217675895446538524670610623369953168412236472302812808639218392319634397138871387898452935081756580084070333246950840091192420542761507705395568904875746222477
#c= 39257649468514605476432946851710016346016992413796229928386230062780829495844059368939749930876895443279723032641876662714088329296631207594999580050131450251288839714711436117326769029649419789323982613380617840218087161435260837263996287628129307328857086987521821533565738409794866606381789730458247531619

题解

https://lazzzaro.github.io/2020/05/06/crypto-RSA/

$dp≡d(mod(p−1))\\ \\ ∵dp⋅e≡d⋅e≡1(mod(p−1))\\ ∴dp⋅e−1=k⋅(p−1)\\ ∴(dp⋅e−1)⋅d⋅e=k′⋅(p−1)\\k′=k⋅d⋅e\\⇔d⋅e=−k′⋅(p−1)+dp⋅e⋅d⋅e≡1(modφ(n))\\ ⇔−k′⋅(p−1)+dp⋅e≡1(modφ(n))\\ ∴k1⋅(p−1)+dp⋅e−1=k2⋅(p−1)⋅(q−1)⇔(p−1)⋅(k2⋅(q−1)−k1)+1=dp⋅e\\ ∵dp<p−1∴(k2⋅(q−1)−k1)∈(0,e)\\$

∴ 遍历 (1,e)，当满足

$n mod((dp⋅e−1)//i+1)==0$

得出p,q

WP

from Crypto.Util.number import *
import gmpy2
e=65537
dp= 5892502924236878675675338970704766304539618343869489297045857272605067962848952532606770917225218534430490745895652561015493032055636004130931491316020329
n= 50612159190225619689404794427464916374543237300894011803225784470008992781409447214236779975896311093686413491163221778479739252804271270231391599602217675895446538524670610623369953168412236472302812808639218392319634397138871387898452935081756580084070333246950840091192420542761507705395568904875746222477
c= 39257649468514605476432946851710016346016992413796229928386230062780829495844059368939749930876895443279723032641876662714088329296631207594999580050131450251288839714711436117326769029649419789323982613380617840218087161435260837263996287628129307328857086987521821533565738409794866606381789730458247531619

for x in range(1, e):
   if(e*dp%x==1):
      p=(e*dp-1)//x+1
      if(n%p!=0):
         continue
      q=n//p
      phin=(p-1)*(q-1)
      d=gmpy2.invert(e, phin)
      m=gmpy2.powmod(c, d, n)
      if(len(hex(m)[2:])%2==1):
         continue
      print(long_to_bytes(m))
#LitCTF{Prim3_1s_Le@k!!!!!}

[LitCTF 2023]The same common divisor

题目

from Crypto.Util.number import *
m=bytes_to_long(b'xxxxxx')
e=65537
p=getPrime(1024)
q1=getPrime(1024)
q2=getPrime(1024)
n1=p*q1
n2=p*q2
c1=pow(m,e,n1)
c2=pow(m,e,n2)
n3=n1^n2
print('n1=',n1)
print('n3=',n3)
print('c1=',c1)
print('c2=',c2)
#n1= 9852079772293301283705208653824307027320071498525390578148444258198605733768947108049676831872672654449631852459503049139275329796717506126689710613873813880735666507857022786447784753088176997374711523987152412069255685005264853118880922539048290400078105858759506186417678959028622484823376958194324034590514104266608644398160457382895380141070373685334979803658172378382884352616985632157233900719194944197689860219335238499593658894630966428723660931647038577670614850305719449893199713589368780231046895222526070730152875112477675102652862254926169713030701937231206405968412044029177246460558028793385980934233
#n3= 4940268030889181135441311597961813780480775970170156650560367030148383674257975796516865571557828263935532335958510269356443566533284856608454193676600884849913964971291145182724888816164723930966472329604608512023988191536173112847915884014445539739070437180314205284883149421228744714989392788108329929896637182055266508625177260492776962915873036873839946591259443753924970795669864031580632650140641456386202636466624658715315856453572441182758855085077441336516178544978457053552156714181607801760605521338788424464551796638531143900048375037218585999440622490119344971822707261432953755569507740550277088437182
#c1= 7066425618980522033304943700150361912772559890076173881522840300333719222157667104461410726444725540513601550570478331917063911791020088865705346188662290524599499769112250751103647749860198318955619903728724860941709527724500004142950768744200491448875522031555564384426372047270359602780292587644737898593450148108629904854675417943165292922990980758572264063039172969633878015560735737699147707712154627358077477591293746136250207139049702201052305840453700782016480965369600667516646007546442708862429431724013679189842300429421340122052682391471347471758814138218632022564279296594279507382548264409296929401260
#c2= 854668035897095127498890630660344701894030345838998465420605524714323454298819946231147930930739944351187708040037822108105697983018529921300277486094149269105712677374751164879455815185393395371001495146490416978221501351569800028842842393448555836910486037183218754013655794027528039329299851644787006463456162952383099752894635657833907958930587328480492546831654755627949756658554724024525108575961076341962292900510328611128404001877137799465932130220386963518903892403159969133882215092783063943679288192557384595152566356483424061922742307738886179947575613661171671781544283180451958232826666741028590085269

题解

n1,n2共享素数p

由于n3=n1^n2

可得n2=n1^n3

p是n1,n2的公约数

求出p

WP

import gmpy2
from Crypto.Util.number import *
e=65537
n1= 9852079772293301283705208653824307027320071498525390578148444258198605733768947108049676831872672654449631852459503049139275329796717506126689710613873813880735666507857022786447784753088176997374711523987152412069255685005264853118880922539048290400078105858759506186417678959028622484823376958194324034590514104266608644398160457382895380141070373685334979803658172378382884352616985632157233900719194944197689860219335238499593658894630966428723660931647038577670614850305719449893199713589368780231046895222526070730152875112477675102652862254926169713030701937231206405968412044029177246460558028793385980934233
n3= 4940268030889181135441311597961813780480775970170156650560367030148383674257975796516865571557828263935532335958510269356443566533284856608454193676600884849913964971291145182724888816164723930966472329604608512023988191536173112847915884014445539739070437180314205284883149421228744714989392788108329929896637182055266508625177260492776962915873036873839946591259443753924970795669864031580632650140641456386202636466624658715315856453572441182758855085077441336516178544978457053552156714181607801760605521338788424464551796638531143900048375037218585999440622490119344971822707261432953755569507740550277088437182
c1= 7066425618980522033304943700150361912772559890076173881522840300333719222157667104461410726444725540513601550570478331917063911791020088865705346188662290524599499769112250751103647749860198318955619903728724860941709527724500004142950768744200491448875522031555564384426372047270359602780292587644737898593450148108629904854675417943165292922990980758572264063039172969633878015560735737699147707712154627358077477591293746136250207139049702201052305840453700782016480965369600667516646007546442708862429431724013679189842300429421340122052682391471347471758814138218632022564279296594279507382548264409296929401260
c2= 854668035897095127498890630660344701894030345838998465420605524714323454298819946231147930930739944351187708040037822108105697983018529921300277486094149269105712677374751164879455815185393395371001495146490416978221501351569800028842842393448555836910486037183218754013655794027528039329299851644787006463456162952383099752894635657833907958930587328480492546831654755627949756658554724024525108575961076341962292900510328611128404001877137799465932130220386963518903892403159969133882215092783063943679288192557384595152566356483424061922742307738886179947575613661171671781544283180451958232826666741028590085269
n2=n3^n1
n2= 13275392358603749049507302824073643158313511157306042129424622043169404438475070367199888792522735816696831092853554043588044629442339762181808939836068784930395387656511731023773900700005021564847480224798180592959510217158765133918150651706674329603149481255390797032771700235015269257730220757739489147426447858665350504461218790022992177725157756735193197648927044824616697206813752794351736481372892433605669363455272775767270738838271685683788851792503697508906872616175734362549442203442409947760416740297996886756365560632301306250478012961270642177511142736084877917270911656025730517314096773424314000497639
p=gmpy2.gcd(n1,n2)
q1=n1//p
q2=n2//p
phi1=(p-1)*(q1-1)
phi2=(p-1)*(q2-1)
d1=gmpy2.invert(e,phi1)
d2=gmpy2.invert(e,phi2)
m=pow(c1,d1,n1)
print(long_to_bytes(m))
#LitCTF{TH3_Tw0_nUmb3rs_H@v3_The_sAme_D1v1s0r!!}

[LitCTF 2023]Euler

题目

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
p = getPrime(512)
q = getPrime(512)
n = p*q
c = pow(m,n-p-q+3,n)
print(f'n = {n}')
print(f'c = {c}')
"""
n = 115140122725890943990475192890188343698762004010330526468754961357872096040956340092062274481843042907652320664917728267982409212988849109825729150839069369465433531269728824368749655421846730162477193420534803525810831025762500375845466064264837531992986534097821734242082950392892529951104643690838773406549
c = 406480424882876909664869928877322864482740577681292497936198951316587691545267772748204383995815523935005725558478033908575228532559165174398668885819826720515607326399097899572022020453298441
"""

题解

提示欧拉定理：
若正整数 a , n 互质，则

$a^{φ(n)}≡1(mod n)$

其中 φ(n) 是欧拉函数（1~n) 与 n 互质的数。

$c = pow(m,n-p-q+3,n)\\ n=p*q\\ \\ \\φ(n)=(p-1)*(q-1)\\ \ \ \ \ =p*q-q-p+1\\ =n-q-p+1$

$c\equiv m^{n-p-q+3} \ \ mod(\ \ n \ \ )$

可变形为

$c\equiv m^{n-p-q+1} *m^2\ \ mod(\ \ n \ \ )$

由欧拉定义可得

$c\equiv m^2\ \ mod(\ \ n \ \ )$

2次方很小，直接爆破

WP

import gmpy2
from Crypto.Util.number import long_to_bytes

n = 115140122725890943990475192890188343698762004010330526468754961357872096040956340092062274481843042907652320664917728267982409212988849109825729150839069369465433531269728824368749655421846730162477193420534803525810831025762500375845466064264837531992986534097821734242082950392892529951104643690838773406549
c = 406480424882876909664869928877322864482740577681292497936198951316587691545267772748204383995815523935005725558478033908575228532559165174398668885819826720515607326399097899572022020453298441
if gmpy2.iroot(c,2)[1]==1:
    m=gmpy2.iroot(c,2)[0]
    print(long_to_bytes(m))
else:
    print("NO result！")

    #LitCTF{a1a8887793acfc199182a649e905daab}

[LitCTF 2023]baby_xor

题目

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
assert len(flag)==32
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537
c1 = p^m
c2 = pow(m,e,n)
print(f'n = {n}')
print(f'c1 = {c1}')
print(f'c2 = {c2}')
"""
n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
c2 = 112016152270171196606652761990170033221036025260883289104273504703557624964071464062375228351458191745141525003775876044271210498526920529385038130932141551598616579917681815276713386113932345056134302042399379895915706991873687943357627747262597883603999621939794450743982662393955266685255577026078256473601
"""

题解

p为512bit，p的高位至少泄露264bit时候，环多项式方程在模n情况下有解,还有8bit，想到头为"LitCTF{"

kbits=512-256-56=200

wp

from tqdm import tqdm
e = 65537
n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
c2 = 112016152270171196606652761990170033221036025260883289104273504703557624964071464062375228351458191745141525003775876044271210498526920529385038130932141551598616579917681815276713386113932345056134302042399379895915706991873687943357627747262597883603999621939794450743982662393955266685255577026078256473601

m = bytes_to_long(b'LitCTF{' + b'\x00'*25)
p_high = (c1^^m)>>200

PR.<x> =Zmod(n)[]
f = (p_high << 200) + x
res = f.small_roots(X = 2^200 ,beta =0.4, epsilon=0.01)
c = res[0] + (p_high<<200)
m = int(c1) ^^ int(c)
print(long_to_bytes(m))
#LitCTF{oh!!!!coppersmith_is_fun}

[LitCTF 2023]隐晦的聊天记录

题目

出题人:6c73d5240a948c86981bc294814d

某不知名收件人：收到消息attack at dawn

出题人:xxxxxxxxxxxxxxxxxxxxxxxxxxxx

某不知名收件人：收到消息Monday or Thur

已知出题人和收件人手中的密钥相同，请解出出题人第二次发送的密文呢（16进制，字母小写，解得的结果记得要加上LitCTF{}哦。）

题解

提示了OPT加密

一次一密（One-time password）

一个序列密码称为一次一密必须满足以下条件：

通过真随机数生成器得到密钥序列s0,s1,s2,…

一次一密的密钥长度必须和明文长度一样。

假设发送方要发送信息M

发送方：

使用ASCII编码M,得到二进制T1

接下来你需要一个和上面二进制串长度完全一致的密钥key

将T1与key进行XOR 运算，得到T2

发送方将T2发送给接收方

接收方：

接收方得到T2将其与key进行XOR运算，得到发送方的数据，再利用ascii编码即可得到正确的信息。

wp

ciphertext1 = bytes.fromhex("6c73d5240a948c86981bc294814d")
plaintext1 = "attack at dawn".encode()
plaintext2 = "Monday or Thur".encode()

key = bytes([a ^ b for a, b in zip(plaintext1, ciphertext1)])
ciphertext2 = bytes([a ^ b for a, b in zip(plaintext2, key)])

print('LitCTF{'+ciphertext2.hex()+'}')
#LitCTF{4068cf2108868c889e1bf29d8351}

[LitCTF 2023]babyLCG

题目

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
bit_len = m.bit_length()
a = getPrime(bit_len)
b = getPrime(bit_len)
p = getPrime(bit_len+1)

seed = m
result = []
for i in range(10):
    seed = (a*seed+b)%p
    result.append(seed)
print(result)
"""
result = [699175025435513913222265085178805479192132631113784770123757454808149151697608216361550466652878, 193316257467202036043918706856603526262215679149886976392930192639917920593706895122296071643390, 1624937780477561769577140419364339298985292198464188802403816662221142156714021229977403603922943, 659236391930254891621938248429619132720452597526316230221895367798170380093631947248925278766506, 111407194162820942281872438978366964960570302720229611594374532025973998885554449685055172110829, 1415787594624585063605356859393351333923892058922987749824214311091742328340293435914830175796909, 655057648553921580727111809001898496375489870757705297406250204329094679858718932270475755075698, 1683427135823894785654993254138434580152093609545092045940376086714124324274044014654085676620851, 492953986125248558013838257810313149490245209968714980288031443714890115686764222999717055064509, 70048773361068060773257074705619791938224397526269544533030294499007242937089146507674570192265]
"""

题解

https://www.cnblogs.com/vancasola/p/9942583.html

LCG（linear congruential generator）线性同余算法，是一个古老的产生随机数的算法。由以下参数组成：

参数	m	a	c	X
性质	模数	乘数	加数	随机数
作用	取模	移位	偏移	作为结果

LCG算法是如下的一个递推公式，每下一个随机数是当前随机数向左移动 log2 a 位，加上一个 c，最后对 m 取余，使随机数限制在 0 ~ m-1 内

python 实现

def lcg(modulus, a, c, seed):
    while True:
        seed = (a * seed + c) % modulus
        yield seed

wp

from Crypto.Util.number import *
def gcd(a,b):
    if(b==0):
        return a
    else:
        return gcd(b,a%b)
s =  [699175025435513913222265085178805479192132631113784770123757454808149151697608216361550466652878, 193316257467202036043918706856603526262215679149886976392930192639917920593706895122296071643390, 1624937780477561769577140419364339298985292198464188802403816662221142156714021229977403603922943, 659236391930254891621938248429619132720452597526316230221895367798170380093631947248925278766506, 111407194162820942281872438978366964960570302720229611594374532025973998885554449685055172110829, 1415787594624585063605356859393351333923892058922987749824214311091742328340293435914830175796909, 655057648553921580727111809001898496375489870757705297406250204329094679858718932270475755075698, 1683427135823894785654993254138434580152093609545092045940376086714124324274044014654085676620851, 492953986125248558013838257810313149490245209968714980288031443714890115686764222999717055064509, 70048773361068060773257074705619791938224397526269544533030294499007242937089146507674570192265]
t = []
for i in range(9):
    t.append(s[i]-s[i-1])
all_n = []
for i in range(7):
    all_n.append(gcd((t[i+1]*t[i-1]-t[i]*t[i]), (t[i+2]*t[i]-t[i+1]*t[i+1])))

MMI = lambda A, n,s=1,t=0,N=0: (n < 2 and t%N or MMI(n, A%n, t, s-A//n*t, N or n),-1)[n<1] #逆元计算
for n in all_n:
    n=abs(n)
    if n==1:
        continue
    a=(s[2]-s[1])*MMI((s[1]-s[0]),n)%n
    ani=MMI(a,n)
    b=(s[1]-a*s[0])%n
    seed = (ani*(s[0]-b))%n
    plaintext=seed
    print(long_to_bytes(plaintext))

'''
b'LitCTF{31fcd7832029a87f6c9f760fcf297b2f}'
b'LitCTF{31fcd7832029a87f6c9f760fcf297b2f}'
b'LitCTF{31fcd7832029a87f6c9f760fcf297b2f}'
b'LitCTF{31fcd7832029a87f6c9f760fcf297b2f}'
b'\x0e\xa3\x083\xfa\x91\x0bh\x88Hn\x84V\x85\x95.\x88\xc8\xbdbL\xf4\xf5\x9b\xc0E\xebo \xea\xf9\xac\x17\x04(/\x0f\xc9\x86s\x04'
'''

[LitCTF 2023]我测你vva

题目

public class Encrypto{
    public static void main(String[] args) {
        String flag="";
        int cipher;
        char[] arr;
        arr=flag.toCharArray();
        for(int i=0; i<flag.length(); i++) {
           if(i%2==0){
            cipher=Integer.valueOf(arr[i]);
            cipher=cipher+i;
            System.out.print((char)cipher);
           }
           if(i%2!=0){
            cipher=Integer.valueOf(arr[i]);
            cipher=cipher-i;
            System.out.print((char)cipher);
           }
        }
    }
}
//cipher=HYEQJvPZ~X@+Bp

题解

加密给你了，逆推一下就可

wp

cipher = "HYEQJvPZ~X@+Bp"
flag = ""
for i in range(len(cipher)):
    if i % 2 == 0:
        flag += chr(ord(cipher[i]) - i)
    else:
        flag += chr(ord(cipher[i]) + i)
print(flag)
#HZCTF{Java666}

[LitCTF 2023]Where is P?

题目

from Crypto.Util.number import *
m=bytes_to_long(b'XXXX')
e=65537
p=getPrime(1024)
q=getPrime(1024)
n=p*q
print(p)
c=pow(m,e,n)
P=p>>340
print(P)
a=pow(P,3,n)
print("n=",n)
print("c=",c)
print("a=",a)
#n= 24479907029118467064460793139240403258697681144532146836881997837526487637306591893357774423547391867013441147680031968367449693796015901951120514250935018725570026327610524687128709707340727799633444550317834481416507364804274266363478822257132586592232042108076935945436358397787891169163821061005102693505011197453089873909085170776511350713452580692963748763166981047023704528272230392479728897831538235554137129584665886878574314566549330671483636900134584707867654841021494106881794644469229030140144595938886437242375435914268001721437309283611088568191856208951867342004280893021653793820874747638264412653721
#c= 6566517934961780069851397787369134601399136324586682773286046135297104713708615112015588908759927424841719937322574766875308296258325687730658550956691921018605724308665345526807393669538103819281108643141723589363068859617542807984954436567078438099854340705208503317269397632214274507740533638883597409138972287275965697689862321166613821995226000320597560745749780942467497435742492468670016480112957715214640939272457886646483560443432985954141177463448896521810457886108311082101521263110578485768091003174683555938678346359150123350656418123918738868598042533211541966786594006129134087145798672161268647536724
#a= 22184346235325197613876257964606959796734210361241668065837491428527234174610482874427139453643569493268653377061231169173874401139203757698022691973395609028489121048788465356158531144787135876251872262389742175830840373281181905217510352227396545981674450409488394636498629147806808635157820030290630290808150235068140864601098322473572121965126109735529553247807211711005936042322910065304489093415276688746634951081501428768318098925390576594162098506572668709475140964400043947851427774550253257759990959997691631511262768785787474750441024242552456956598974533625095249106992723798354594261566983135394923063605

题解

爆破P，开三次，求出P

P=p>>340

可知p的高位泄露（1024-340= 684 位），Coppersmith恢复p

WP

import gmpy2
from Crypto.Util.number import *

e=65537
n= 24479907029118467064460793139240403258697681144532146836881997837526487637306591893357774423547391867013441147680031968367449693796015901951120514250935018725570026327610524687128709707340727799633444550317834481416507364804274266363478822257132586592232042108076935945436358397787891169163821061005102693505011197453089873909085170776511350713452580692963748763166981047023704528272230392479728897831538235554137129584665886878574314566549330671483636900134584707867654841021494106881794644469229030140144595938886437242375435914268001721437309283611088568191856208951867342004280893021653793820874747638264412653721
c= 6566517934961780069851397787369134601399136324586682773286046135297104713708615112015588908759927424841719937322574766875308296258325687730658550956691921018605724308665345526807393669538103819281108643141723589363068859617542807984954436567078438099854340705208503317269397632214274507740533638883597409138972287275965697689862321166613821995226000320597560745749780942467497435742492468670016480112957715214640939272457886646483560443432985954141177463448896521810457886108311082101521263110578485768091003174683555938678346359150123350656418123918738868598042533211541966786594006129134087145798672161268647536724
a= 22184346235325197613876257964606959796734210361241668065837491428527234174610482874427139453643569493268653377061231169173874401139203757698022691973395609028489121048788465356158531144787135876251872262389742175830840373281181905217510352227396545981674450409488394636498629147806808635157820030290630290808150235068140864601098322473572121965126109735529553247807211711005936042322910065304489093415276688746634951081501428768318098925390576594162098506572668709475140964400043947851427774550253257759990959997691631511262768785787474750441024242552456956598974533625095249106992723798354594261566983135394923063605
for i in range(100000):
    if gmpy2.iroot(i * n + a, 3)[1]==True:
        P = gmpy2.iroot(i * n + a, 3)[0]
        print(f'P={P}')
        break
p4=66302204855869216148926460265779698576660998574555407124043768605865908069722142097621926304390549253688814246272903647124801382742681337653915017783954290069842646020090511605930590064443141710086879668946

'''pbits = 1024
kbits = 340
print(p4.nbits())
p4 = p4 << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X=2^kbits, beta=0.4)
#经过以上一些函数处理后，n和p已经被转化为10进制
if roots:
   p = p4+int(roots[0])
   print("p: "+str(p))'''

p=148500014720728755901835170447203030242113125689825190413979909224639701026120883281188694701625473553602289432755479244507504340127322979884849883842306663453018960250560834067472479033116264539127330613635903666209920113813160301513820286874124210921593865507657148933555053341577090100101684021531775022459
q=n//p
phi=(p-1)*(q-1)
d=inverse(e,phi)
m=pow(c,d,n)
print(long_to_bytes(m))
#LitCTF{Y0U_hAV3_g0T_Th3_r1ghT_AnsW3r}