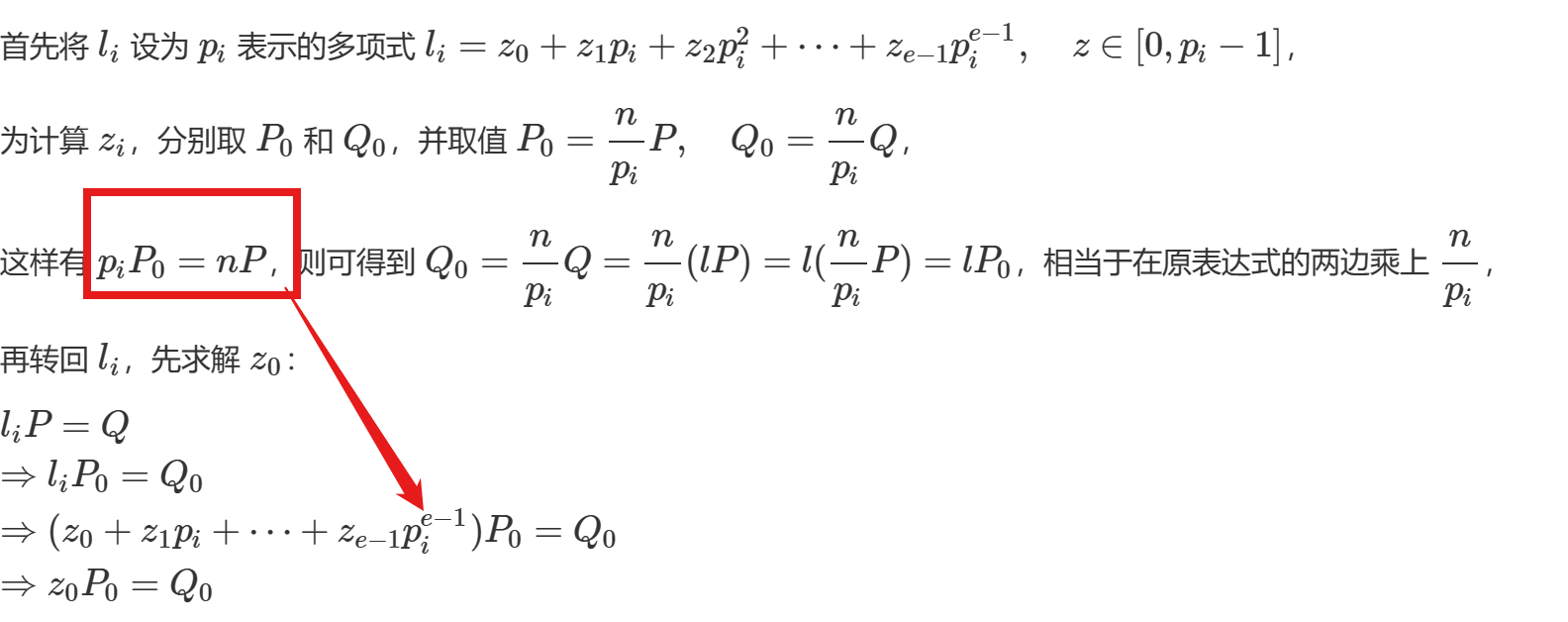ECC

ECC | Lazzaro (lazzzaro.github.io)

椭圆曲线加密算法最通俗的解释 不需要数学基础（2）ECC加密算法_哔哩哔哩_bilibili

基本概念

椭圆曲线不是椭圆而是椭圆积分方程

一条椭圆曲线是在射影平面上满足威尔斯特拉斯方程（Weierstrass）所有点的集合

• 椭圆曲线的定义式：

  $y2+axy+by=x3+cx2+dx+e$

  一般方程：

  $y2+a1xy+a3y=x3+a2x2+a4x+a6$

• 1椭圆曲线方程是一个齐次方程

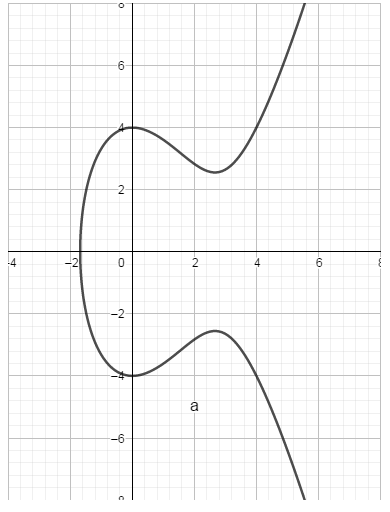
• 椭圆曲线都是关于X轴对称的曲线。

• 2曲线上的每个点都必须是非奇异的（光滑的），偏导数FX(X,Y,Z)、FY(X,Y,Z)、FZ(X,Y,Z)不同为0

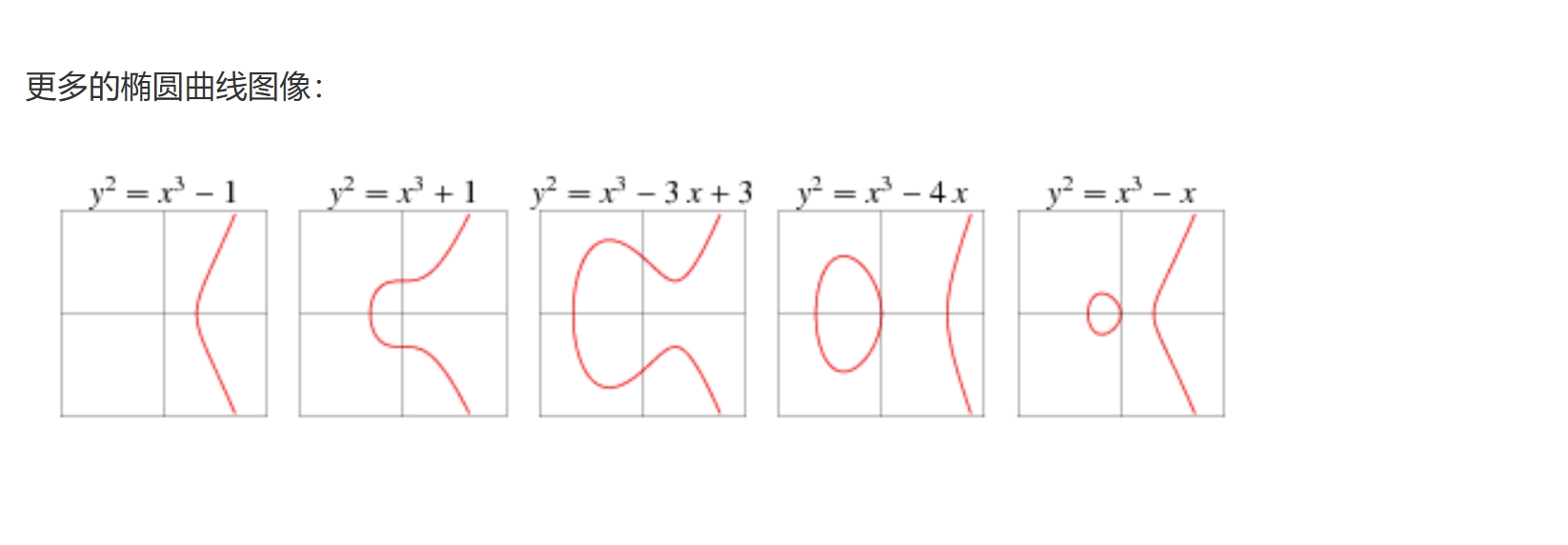
• 3圆曲线的形状，并不是椭圆的。只是因为椭圆曲线的描述方程，类似于计算一个椭圆周长的方程故得名

• 椭圆曲线表达式

  ${(x,y)∈R2∣y2=x^3+ax+b,4a^3+27b^2≠0}∪{O}$

加法运算规则

P,Q,R如果在一条直线上，并且在椭圆曲线上，那么P+Q+R=0(椭圆曲线阿尔贝群)

为了避免p点没有切线，因此要满足

$判别式：4*a^3+37*b^2\ne 0$

$加法运算法则\\0\oplus0=0\\ P\oplus0=0\oplus P=P\\ P\oplus(-P)=0\\ P为(x,y)\\-P为(x,-y)\\两点关于x轴对称 \\ \oplus满足交换律，结合律$

代数加法

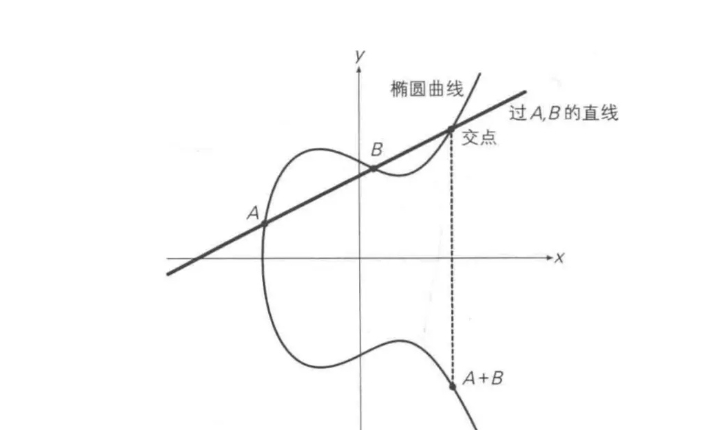
几何加法

加法

A+B

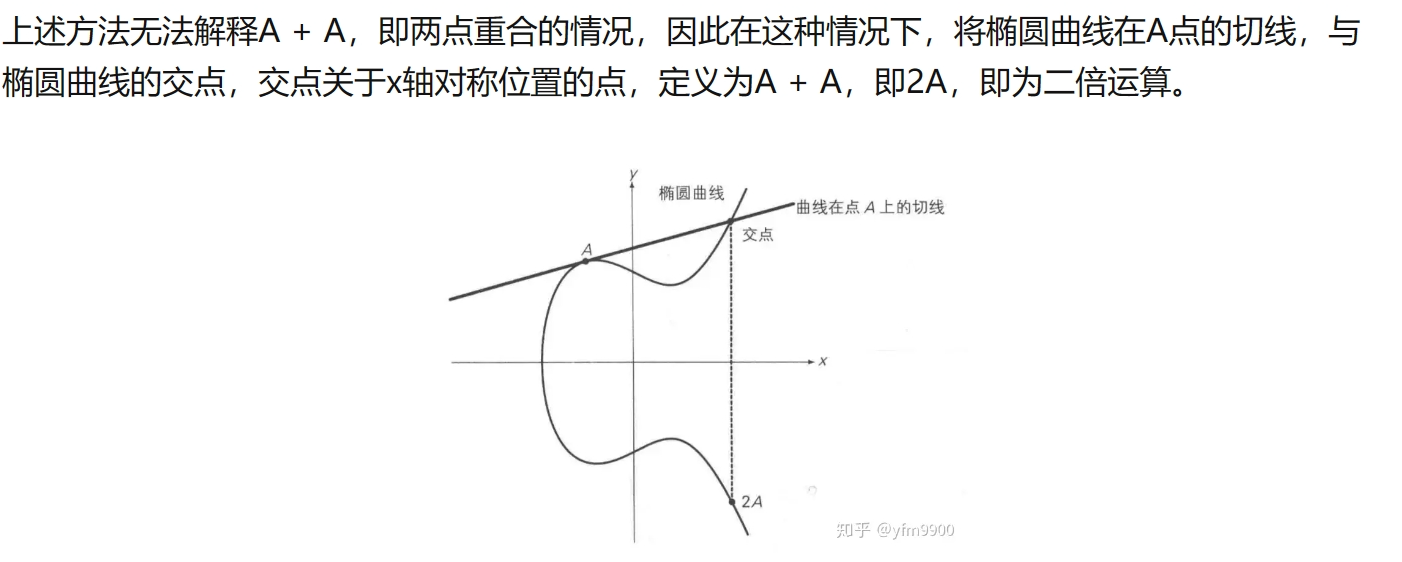
二倍运算

2A

普通相交三点：P+Q+R=0

普通相交两点：P+P+Q=0，P+Q+Q=0 （一点相切）

垂直相交两点：P+Q+0=0 （垂直X轴）

垂直相交一点：P+P+0=0 （垂直X轴+一点相切）

离散化

椭圆曲线密码体制使用的是有限域上的椭圆曲线，即变量和代数为有限域中的元素。有限域GF（p）上的椭圆曲线是指满足方程

$y^2\equiv x^3+ax+b(mod p)$

的所有点再加上一个无穷远点O构成的集合，其中a，b,x,y均在有限域上取值，p是素数。记为Ep(a,b)

椭圆曲线上的阶：椭圆曲线中元素的个数，表示|Ep(a,b)|

椭圆曲线上元素的阶： 记为ord§，令nP=O（无穷远点）的最小整数。

生成元： ord(G)=|Ep(a,b)|,则称G为Ep(a,b)的生成元,

椭圆曲线上的离散对数问题

$如果已知Y,G,求满足Y=kG的k,0\le k \le ord(G),\\ 其中G是有限域Zp上Ep(a,b)的生成元,\\Y是有限域Zp上的椭圆曲线上的一点$

ECC算法

参数选取：选定一条椭圆曲线 Ep(a,b)，并取椭圆曲线上一点作为基点 G；(G是Ep(a,b)的生成元)

产生公钥和私钥：选择一个私有密钥 Sk (k<n)，并生成公开密钥 Pk=SkG；

加密：将明文编码到 Ep(a,b)上的一点 M，并产生一个随机整数 r（0<r<n，n为 G 的阶数）；C1=(C1,C2),C1=M+rPk和 C2=rG

解密：

M=C2-SkC1

C2-SkC1=M+rPk-SkrG=M+rSkG-SkrG=M

常见攻击

Smart’s attack

适用于：E.order()=p

即一个椭圆曲线的阶等于 p，意味着曲线上的点的数量与有限域的元素数量相同

p=h*n的椭圆曲线

脚本：

p = 
A = 
B = 
E = EllipticCurve(GF(p),[A,B])##确定椭圆曲线
#给出两点P,Q
P = E(,)
Q = E(,)
def SmartAttack(P,Q,p):#寻找k
    E = P.curve()
    #构造扰动后的椭圆曲线
    Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])

    P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
    for P_Qp in P_Qps:
        if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
            break

    Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
    for Q_Qp in Q_Qps:
        if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
            break

    p_times_P = p*P_Qp
    p_times_Q = p*Q_Qp

    # 获取 pP 和 pQ 的坐标
    x_P,y_P = p_times_P.xy()
    x_Q,y_Q = p_times_Q.xy()

    phi_P = -(x_P/y_P)
    phi_Q = -(x_Q/y_Q)
    #计算离散对数 k = phi_Q / phi_P
    k = phi_Q/phi_P
    return ZZ(k)

r = SmartAttack(P, Q, p)
print(r)

Pohlig-Hellman算法

主要解决：整数域中

$y=g^x(modp)$

里的 x以及椭圆曲线离散对数问题中 Gk=Q的 G的阶 n

P的阶n: nP=O

Q mod nP =l

Q mod n=l

Q 模上n的因数等于l

寻找在不同因子下的l的对应同余数li

脚本

#Sage Code 1
p = 
a = 
b = 
#G P 两点坐标
gx = 
gy = 
px = 
py = 

E = EllipticCurve(GF(p), [a, b])
G = E(gx, gy)
n = E.order()
QA = E(px, py)

#n 的素因子
factors = list(factor(n))
m = 1
moduli = []
remainders = []

print(f"[+] Running Pohlig Hellman")
print(factors)


for i, j in factors:
    if i > 10**9:
        print(i)
        break
    mod = i**j
    g2 = G*(n//mod)#G0
    q2 = QA*(n//mod)#Q0
    #discrete_log离散对数LiP0=Q
    r = discrete_log(q2, g2, operation='+')
    remainders.append(r)
    moduli.append(mod)
    m *= mod
    
#中国剩余定理
r = crt(remainders, moduli)
print(r)
#求出L,相当于求解出私钥

#Sage Code 2
E = EllipticCurve(GF(p), [a, b])
P = E()
Q = E()

factors, exponents = zip(*factor(E.order()))
#factor(E.order())返回了一个由因子和指数组成的元组列表,zip将因子和指数分别放入两个独立的元组中。
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-2]
print(primes)
dlogs = []
for fac in primes:
	t = int(int(P.order()) // int(fac))
	dlog = discrete_log(t*Q,t*P,operation="+")
    #t*Q=Q0
	dlogs += [dlog]#li
	print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) 

l = crt(dlogs,primes)
print(l)

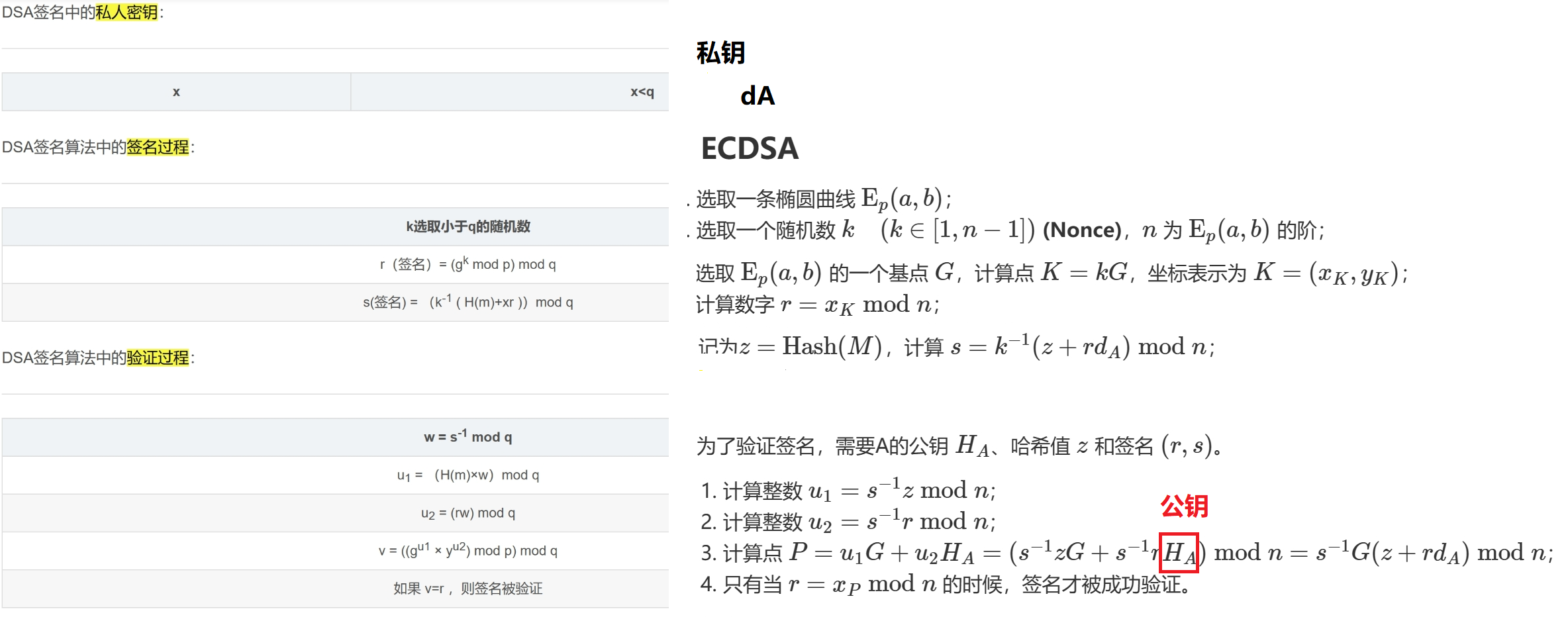
ECDSA

ECDSA（Elliptic Curve Digital Signature Algorithm）是一种基于椭圆曲线密码学的数字签名算法。它是公钥密码学体系中的一部分，用于生成和验证数字签名