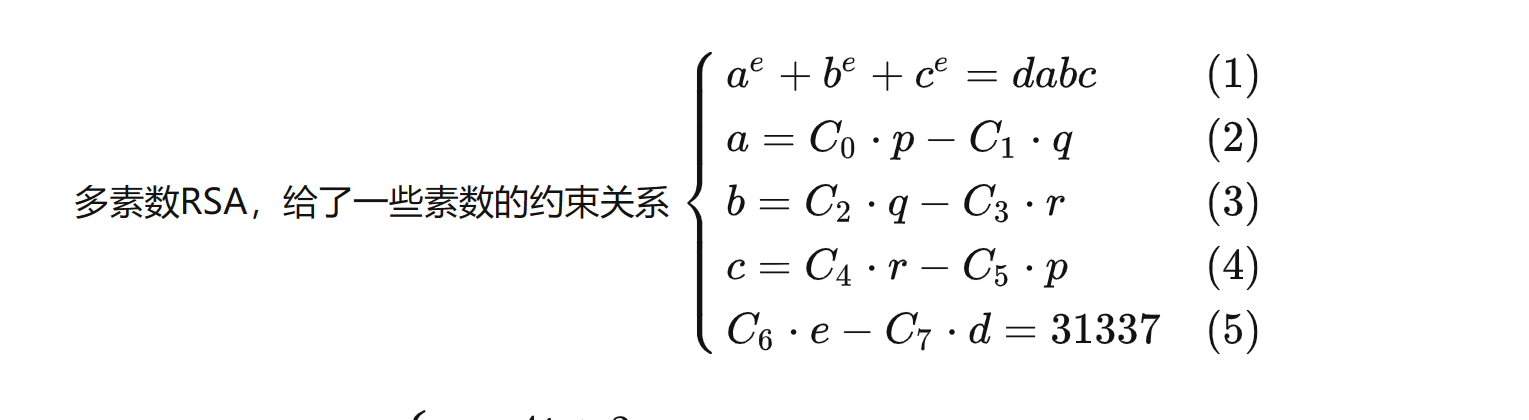[CryptoCTF2023 (part1) - ZimaB1ue - 博客园 (cnblogs.com)

[CryptoCTF 2023 | LOV3 (lov2.netlify.app)](https://www.cnblogs.com/ZimaBlue/articles/17538563.html)

Easy

Did it!

题目

Finding the intersection among subsets can sometimes be a challenging endeavor, as it requires meticulous comparison and analysis of overlapping elements within each set. But she did it! Try doing it yourself too.

#!/usr/bin/env python3

from random import randint
import sys
from flag import flag

def die(*args):
	pr(*args)
	quit()

def pr(*args):
	s = " ".join(map(str, args))
	sys.stdout.write(s + "\n")
	sys.stdout.flush()

def sc():
	return sys.stdin.buffer.readline()

def did(n, l, K, A):
	A, K = set(A), set(K)
	R = [pow(_, 2, n) + randint(0, 1) for _ in A - K]
	return R

def main():
	border = "+"
	pr(border*72)
	pr(border, ".::   Hi all, she DID it, you should do it too! Are you ready? ::.  ", border)
	pr(border*72)

	_flag = False
	n, l = 127, 20
	N = set(list(range(0, n)))
	K = [randint(0, n-1) for _ in range(l)]
	cnt, STEP = 0, 2 * n // l - 1
	
	while True:
		ans = sc().decode().strip()
		try:
			_A = [int(_) for _  in ans.split(',')]
			if len(_A) <= l and set(_A).issubset(N):
				DID = did(n, l, K, _A)
				pr(border, f'DID = {DID}')
				if set(_A) == set(K):
					_flag = True
			else:
				die(border, 'Exception! Bye!!')
		except:
			die(border, 'Your input is not valid! Bye!!')
		if _flag:
			die(border, f'Congrats! the flag: {flag}')
		if cnt > STEP:
			die(border, f'Too many tries, bye!')
		cnt += 1

if __name__ == '__main__':
	main()

题解

这是一道有远端的题，需要找到一组集合A与预设的K集合相同。

每次输入长度不大于20的集合AA，可以返回K-AA集合中元素i^2+randint(0,1)的结果。

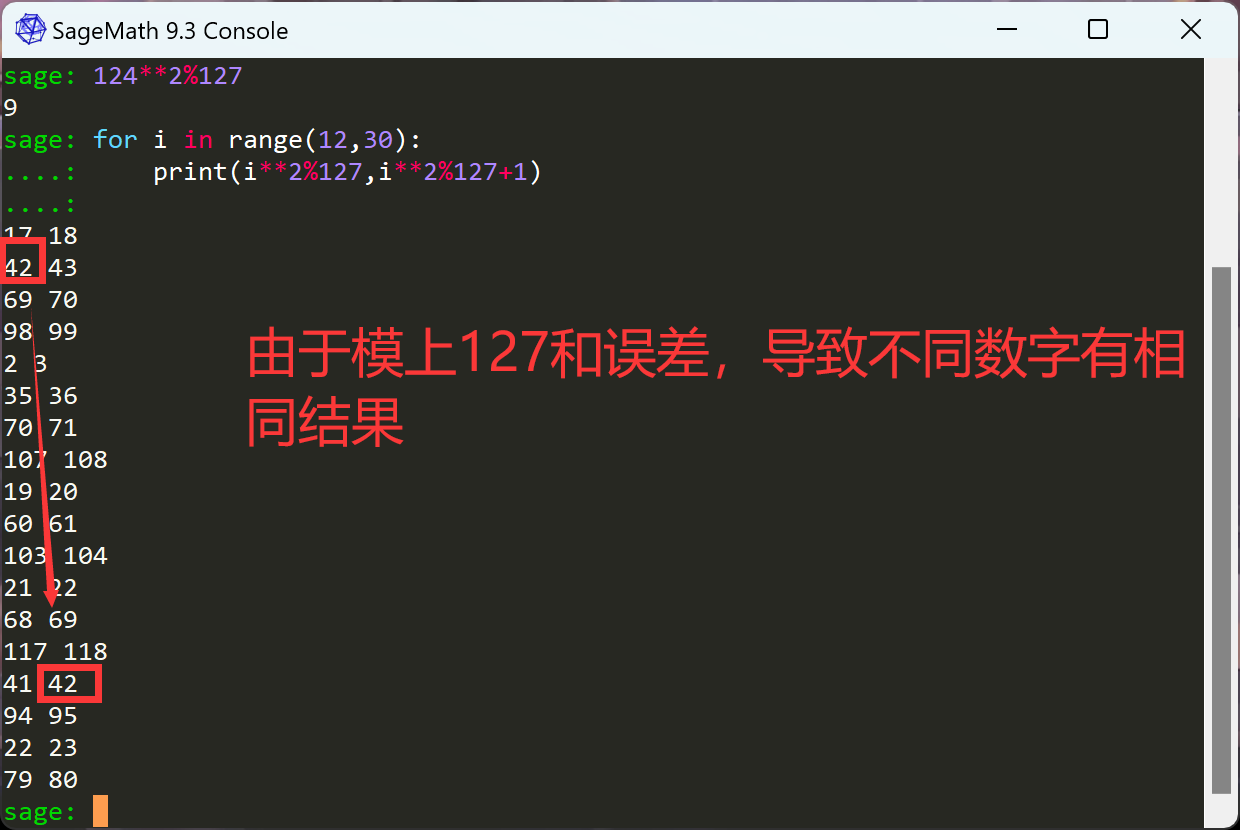
做题的时候，一开始没有考虑到不同数字有相同的结果，直接将0-126数字分7组,手撸出的结果，然后没给出flag，就想到不同数字有相同的结果，还要重来，不会用pwntools库,哭死，不想写了

正解：

image-20230710114150369

所以要将0-126正确分组，使每一组中的元素，不再存在误解（即返回的i**2（mod 127）结果相同），而且保证每组长度不大于20。

先分组

1.按照item中的元素与（1，len(item））无干扰元素分组

n, l = 127, 20
q = []
a = []
for i in range(n):
    for item in q:
        if len(item) >= l:
            continue
        okIn = True
        for k in range(len(item)):
            #按照item中的元素与（1，len(item））无干扰元素分组
            if (i**2 - k**2) % n in [n - 1, 0, 1]:
                okIn = False
                break
        if okIn:
            item.append(i)
            break
    else:
        q.append([i])
    if len(q) >= l:
        a.append(q)
        q = []
a.append(q)
print(a)
'''[[[0, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15, 18, 19, 20, 21, 22, 23],
[1, 12, 17, 24, 25, 26, 27, 28, 29, 30, 31, 33, 34, 38, 39, 40, 41, 42, 43, 44], 
[16, 32, 35, 36, 37, 45, 46, 47, 48, 49, 50, 51, 55, 56, 57, 58, 59, 60, 61, 63], 
[52, 53, 54, 62, 64, 65, 66, 67, 68, 69, 70, 71, 72, 76, 77, 78, 81, 83, 84, 85], 
[73, 74, 75, 79, 80, 82, 86, 87, 88, 89, 90, 93, 94, 96, 97, 98, 99, 100, 102, 104],
[91, 92, 95, 101, 103, 105, 106, 107, 108, 109, 112, 113, 114], [110, 111, 115, 116, 117, 118, 119, 120], [121, 122, 123, 124], [125],
[126]]
]'''

2.找到did处理后返回的值对应的数字，相同返回值作为一个列表,依次从不同列表（长度最大开始）挑选一个值作为一组，每组 长度不超过20

n = 127

a = [[] for i in range(127)]
for i in range(127):
    a[i * i % n].append(i)
    a[i * i % n + 1].append(i)
print(a)
#a中存的是经过did后可能返回的值对应的数字（0，126）
##[[0], [0, 1, 126], [1, 16, 111, 126], [16, 111], [2, 125], [2, 125], [], [], [32, 95], [3, 32, 95, 124], [3, 124], [30, 97], [30, 97], [34, 93], [34, 93], [53, 74], [4, 53, 74, 123], [4, 12, 115, 123], [12, 48, 79, 115], [20, 48, 79, 107], [20, 107], [23, 104], [23, 28, 99, 104], [28, 99], [], [5, 122], [5, 36, 91, 122], [36, 91], [], [], [41, 86], [41, 44, 83, 86], [44, 63, 64, 83], [63, 64], [62, 65], [17, 62, 65, 110], [6, 17, 110, 121], [6, 52, 75, 121], [52, 61, 66, 75], [61, 66], [], [26, 101], [13, 26, 101, 114], [13, 114], [60, 67], [60, 67], [], [38, 89], [38, 89], [7, 120], [7, 47, 80, 120], [47, 80], [59, 68], [59, 68], [], [], [], [], [], [], [21, 106], [21, 51, 76, 106], [51, 58, 69, 76], [58, 69], [8, 119], [8, 119], [], [], [24, 103], [14, 24, 103, 113], [14, 18, 109, 113], [18, 43, 84, 109], [31, 43, 84, 96], [31, 33, 94, 96], [33, 57, 70, 94], [57, 70], [40, 87], [40, 87], [], [29, 98], [29, 98], [9, 118], [9, 35, 92, 118], [35, 92], [46, 81], [46, 81], [], [50, 77], [50, 56, 71, 77], [56, 71], [], [], [], [], [27, 100], [27, 100], [], [], [15, 112], [15, 37, 90, 112], [10, 37, 90, 117], [10, 117], [], [22, 105], [22, 55, 72, 105], [55, 72], [], [19, 108], [19, 108], [], [], [], [], [42, 85], [42, 85], [49, 78], [49, 78], [25, 102], [25, 102], [], [45, 82], [11, 45, 82, 116], [11, 54, 73, 116], [54, 73], [39, 88], [39, 88], []]
#a[1]，经过did处理后可能返回1的数字：0，1，126
# [len(a[i]) for i in range(127)]
# 从最大长度里取值
K = []
for _ in range(7):
    #记录每组互不干扰的值
    tmp = []
    #use记录did处理后的值
    used = []
    while len(tmp) < 20:
        #找到未使用的最大长度列表
        l = max([len(a[i]) for i in range(127) if i not in used])
        if l == 0:
            break
        for i in range(127):
            #将其中的元素添加到临时列表 tmp 中，并记录已使用的元素值。
            # 同时，移除其他列表中与已使用元素值相同的元素，并更新 used 列表。
            if len(a[i]) == l and i not in used:
                #移除列表最后一个元素，并赋值给v
                v = a[i].pop()
                tmp.append(v)
                used.append(v * v % n)
                used.append(v * v % n + 1)
                for j in range(127):
                    if v in a[j]:
                        a[j] = [ii for ii in a[j] if ii != v]
                break
    #print(tmp)
                # K.append(','.join([str(i) for i in tmp]))
    K.append([i for i in tmp])

print(K)

WP

n = 127

a = [[] for i in range(127)]
for i in range(127):
    a[i * i % n].append(i)
    a[i * i % n + 1].append(i)
print(a)
#a中存的是经过did后可能返回的值对应的数字（0，126）
##[[0], [0, 1, 126], [1, 16, 111, 126], [16, 111], [2, 125], [2, 125], [], [], [32, 95], [3, 32, 95, 124], [3, 124], [30, 97], [30, 97], [34, 93], [34, 93], [53, 74], [4, 53, 74, 123], [4, 12, 115, 123], [12, 48, 79, 115], [20, 48, 79, 107], [20, 107], [23, 104], [23, 28, 99, 104], [28, 99], [], [5, 122], [5, 36, 91, 122], [36, 91], [], [], [41, 86], [41, 44, 83, 86], [44, 63, 64, 83], [63, 64], [62, 65], [17, 62, 65, 110], [6, 17, 110, 121], [6, 52, 75, 121], [52, 61, 66, 75], [61, 66], [], [26, 101], [13, 26, 101, 114], [13, 114], [60, 67], [60, 67], [], [38, 89], [38, 89], [7, 120], [7, 47, 80, 120], [47, 80], [59, 68], [59, 68], [], [], [], [], [], [], [21, 106], [21, 51, 76, 106], [51, 58, 69, 76], [58, 69], [8, 119], [8, 119], [], [], [24, 103], [14, 24, 103, 113], [14, 18, 109, 113], [18, 43, 84, 109], [31, 43, 84, 96], [31, 33, 94, 96], [33, 57, 70, 94], [57, 70], [40, 87], [40, 87], [], [29, 98], [29, 98], [9, 118], [9, 35, 92, 118], [35, 92], [46, 81], [46, 81], [], [50, 77], [50, 56, 71, 77], [56, 71], [], [], [], [], [27, 100], [27, 100], [], [], [15, 112], [15, 37, 90, 112], [10, 37, 90, 117], [10, 117], [], [22, 105], [22, 55, 72, 105], [55, 72], [], [19, 108], [19, 108], [], [], [], [], [42, 85], [42, 85], [49, 78], [49, 78], [25, 102], [25, 102], [], [45, 82], [11, 45, 82, 116], [11, 54, 73, 116], [54, 73], [39, 88], [39, 88], []]
#a[1]，经过did处理后可能返回1的数字：0，1，126
# [len(a[i]) for i in range(127)]
# 从最大长度里取值
K = []
for _ in range(7):
    #记录每组互不干扰的值
    tmp = []
    #use记录did处理后的值
    used = []
    while len(tmp) < 20:
        #找到未使用的最大长度列表
        l = max([len(a[i]) for i in range(127) if i not in used])
        if l == 0:
            break
        for i in range(127):
            #将其中的元素添加到临时列表 tmp 中，并记录已使用的元素值。
            # 同时，移除其他列表中与已使用元素值相同的元素，并更新 used 列表。
            if len(a[i]) == l and i not in used:
                #移除列表最后一个元素，并赋值给v
                v = a[i].pop()
                tmp.append(v)
                used.append(v * v % n)
                used.append(v * v % n + 1)
                for j in range(127):
                    if v in a[j]:
                        a[j] = [ii for ii in a[j] if ii != v]
                break
    #print(tmp)
                # K.append(','.join([str(i) for i in tmp]))
    K.append([i for i in tmp])

print(K)

'''for v in K:
    t = eval(str(v))
    s = []
    for i in t:
        s.append(i * i % n)
        s.append(i * i % n + 1)
    print(s)
#[1, 2, 9, 10, 16, 17, 17, 18, 19, 20, 21, 22, 25, 26, 30, 31, 31, 32, 35, 36, 36, 37, 37, 38, 42, 43, 49, 50, 60, 61, 61, 62, 69, 70, 70, 71, 72, 73, 73, 74]
#[81, 82, 87, 88, 98, 99, 100, 101, 103, 104, 121, 122, 2, 3, 8, 9, 15, 16, 18, 19, 22, 23, 26, 27, 32, 33, 34, 35, 38, 39, 41, 42, 50, 51, 62, 63, 68, 69, 71, 72]
#[74, 75, 82, 83, 88, 89, 99, 100, 104, 105, 120, 121, 122, 123, 1, 2, 4, 5, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 18, 19, 22, 23, 26, 27, 31, 32, 34, 35, 35, 36]
#[37, 38, 41, 42, 44, 45, 47, 48, 50, 51, 52, 53, 61, 62, 64, 65, 68, 69, 70, 71, 71, 72, 73, 74, 76, 77, 79, 80, 82, 83, 84, 85, 88, 89, 94, 95, 99, 100, 104, 105]
#[107, 108, 113, 114, 115, 116, 117, 118, 120, 121, 122, 123, 124, 125, 0, 1, 2, 3, 4, 5, 9, 10, 11, 12, 13, 14, 16, 17, 19, 20, 21, 22, 25, 26, 30, 31, 32, 33, 36, 37]
#[38, 39, 42, 43, 44, 45, 47, 48, 49, 50, 52, 53, 60, 61, 62, 63, 64, 65, 69, 70, 72, 73, 74, 75, 76, 77, 79, 80, 81, 82, 84, 85, 87, 88, 94, 95, 98, 99, 100, 101]
#[103, 104, 107, 108, 113, 114, 115, 116, 117, 118, 121, 122, 124, 125]
'''


from pwn import *

p = remote('00.cr.yp.toc.tf', 11337)


#接收三行
p.recvline()
p.recvline()
p.recvline()

n = 127
KP = [[126, 124, 123, 115, 107, 104, 122, 86, 83, 110, 121, 75, 114, 120, 106, 76, 113, 109, 96, 94],
      [118, 77, 112, 117, 105, 116, 111, 95, 74, 79, 99, 91, 64, 65, 66, 101, 80, 69, 103, 84],
      [70, 92, 71, 90, 72, 82, 73, 1, 125, 32, 97, 93, 53, 12, 48, 28, 36, 44, 62, 17],
      [52, 26, 67, 89, 47, 68, 51, 119, 24, 18, 43, 33, 87, 98, 35, 81, 56, 100, 37, 55],
      [108, 85, 78, 102, 45, 54, 88, 0, 16, 2, 3, 30, 34, 4, 20, 23, 5, 41, 63, 6],
      [61, 13, 60, 38, 7, 59, 21, 58, 8, 14, 31, 57, 40, 29, 9, 46, 50, 27, 15, 10],
      [22, 19, 42, 49, 25, 11, 39]]

K = []
for kk in KP:
    #将列表 kk 中的元素转换为字符串，并以逗号分隔，然后将该字符串编码为字节流并发送
    p.sendline(','.join(map(str, kk)).encode())
    #读到DID=出现为止
    p.recvuntil(b'DID = ')
    #接收字节流数据，并将其转换为列表v
    v = eval(p.recvline().strip().decode())
    #筛选出不在交集的元素
    for tk in kk:
        r = tk * tk % n
        if (r not in v) and (r + 1 not in v):
            K.append(str(tk))

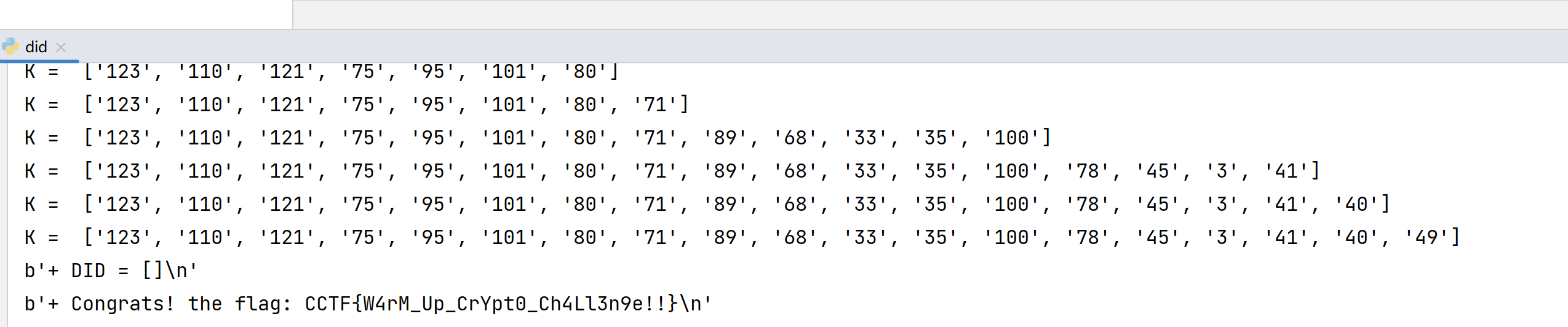
    print('K = ', K)
    if len(K) == 20:
        break

p.sendline((','.join(K)).encode())
print(p.recvline())
print(p.recvline())

# CCTF{W4rM_Up_CrYpt0_Ch4Ll3n9e!!}

image-20230710151730392

image-20230710151404019

blue_office

题目

#!/usr/bin/enc python3

import binascii
from secret import seed, flag

def gen_seed(s):
	i, j, k = 0, len(s), 0
	while i < j:
		k = k + ord(s[i])
		i += 1
	i = 0
	while i < j:
		if (i % 2) != 0:
			k = k - (ord(s[i]) * (j - i + 1))            
		else:
			k = k + (ord(s[i]) * (j - i + 1))
	
		k = k % 2147483647
		i += 1

	k = (k * j) % 2147483647
	return k

def reseed(s):
	return s * 214013 + 2531011

def encrypt(s, msg):
	assert s <= 2**32
	c, d = 0, s
	enc, l = b'', len(msg)
	while c < l:
		d = reseed(d)
		enc += (msg[c] ^ ((d >> 16) & 0xff)).to_bytes(1, 'big')
		c += 1
	return enc

enc = encrypt(seed, flag)
print(f'enc = {binascii.hexlify(enc)}')

题解

爆破seed

改了d, 写成了d= (s- 2531011)//224013,爆破一天都没出来，不知道当时脑子在干嘛(遍历完都没出结果，很懵，没仔细写代码)

s <= 2**32

按照源代码爆破seed

wp

import binascii
from tqdm import trange

enc = binascii.unhexlify(b'b0cb631639f8a5ab20ff7385926383f89a71bbc4ed2d57142e05f39d434fce')

def reseed(s):
    return s * 214013 + 2531011

def decrypt(s, enc):
    c, d = 0, s
    dec, l = b'', len(enc)
    while c < l:
        d = reseed(d)
        dec += (enc[c] ^ ((d >> 16) & 0xff)).to_bytes(1, 'big')
        c += 1
    return dec

for seed in trange(2**32):
    flag = decrypt(seed, enc)
    if b'CCTF{' in flag:
        print(f'Found flag: {flag}')
        break

suction

题目

#!/usr/bin/env python3

from Crypto.Util.number import *
from flag import flag

def keygen(nbit, r):
	while True:
		p, q = [getPrime(nbit) for _ in '__']
		e, n = getPrime(16), p * q
		phi = (p - 1) * (q - 1)
		if GCD(e, phi) == 1:
			N = bin(n)[2:-r]
			E = bin(e)[2:-r]
			PKEY = N + E
			pkey = (n, e)
			return PKEY, pkey

def encrypt(msg, pkey, r):
	m = bytes_to_long(msg)
	n, e = pkey
	c = pow(m, e, n)
	C = bin(c)[2:-r]
	return C

r, nbit = 8, 128
PKEY, pkey = keygen(nbit, r)
print(f'PKEY = {int(PKEY, 2)}')
FLAG = flag.lstrip(b'CCTF{').rstrip(b'}')
enc = encrypt(FLAG, pkey, r)
print(f'enc = {int(enc, 2)}')

#PKEY = 55208723145458976481271800608918815438075571763947979755496510859604544396672=n+e
#ENC = 127194641882350916936065994389482700479720132804140137082316257506737630761

题解

N = bin(n)[2:-r]
E = bin(e)[2:-r]
PKEY = N + E

以为PKEY是n去掉8位与e去掉八位相加的结果

结果…

image-20230710155629038

c,n,e后八位未知,爆破n,c,e。爆破n同时需要调用factordb的api来分解n，直到获得2个128位比特的素数因子。

已知e是16位，去掉八位，he=int(bin(PKEY)[-8:], 2) << 8

from ecdsa.numbertheory import next_prime

PKEY = 55208723145458976481271800608918815438075571763947979755496510859604544396672
ENC = 127194641882350916936065994389482700479720132804140137082316257506737630761

# 部分nec
hn = int(bin(PKEY)[2:-8], 2) << 8
he = int(bin(PKEY)[-8:], 2) << 8
#print(int(bin(PKEY)[2:-8], 2))
#215659074786949126879967971128589122804982702202921795919908245545330251549
#print(hn)
#55208723145458976481271800608918815438075571763947979755496510859604544396544

# 可能的n
plist = [3]#100000以内所有素数
for i in range(100000):
    plist.append(next_prime(plist[-1]))
for i in range(1, 2**8, 2):
    tn = hn + i
    #步长为2保证n是素数
    for v in plist:
        if tn % v == 0:
            #保证n能被分解两个128bit的p,q
            break
    else:
        if not isPrime(tn):
            print(tn)

'''
#找到所有可能的N
55208723145458976481271800608918815438075571763947979755496510859604544396571
55208723145458976481271800608918815438075571763947979755496510859604544396577
55208723145458976481271800608918815438075571763947979755496510859604544396583
55208723145458976481271800608918815438075571763947979755496510859604544396589
55208723145458976481271800608918815438075571763947979755496510859604544396603
55208723145458976481271800608918815438075571763947979755496510859604544396613
55208723145458976481271800608918815438075571763947979755496510859604544396633
55208723145458976481271800608918815438075571763947979755496510859604544396643
55208723145458976481271800608918815438075571763947979755496510859604544396667
'''

找到n

然后爆破e,和c

wp

import gmpy2
from Crypto.Util.number import*

PKEY = 55208723145458976481271800608918815438075571763947979755496510859604544396672
ENC = 127194641882350916936065994389482700479720132804140137082316257506737630761

he = int(bin(PKEY)[-8:], 2) << 8
n = 55208723145458976481271800608918815438075571763947979755496510859604544396613
p = 292926085409388790329114797826820624883
q = 188473222069998143349386719941755726311
phi = (p - 1) * (q - 1)
hc = ENC<<8
# 可能的e
for i in range(2**8):
    for j in range(2**8):
        c = hc + i
        e = he + j
        if not isPrime(e):
            continue
        d = inverse(e,phi)
        flag = long_to_bytes(pow(c,d,n))
        try:
            print(flag.decode())
        except:
            continue

# 6oRYGy&Dc$G2ZS

Medium

Derik

题目


from Crypto.Util.number import *
from secret import C, e, d, p, q, r, flag

O = [1391526622949983, 2848691279889518, 89200900157319, 31337]

assert isPrime(e) and isPrime(d) and isPrime(p) and isPrime(q) and isPrime(r)
assert C[0] * p - C[1] * q >= 0
assert C[2] * q - C[3] * r >= 0
assert C[4] * r - C[5] * p >= 0
assert (C[0] * p - C[1] * q) ** e + (C[2] * q - C[3] * r) ** e + (C[4] * r - C[5] * p) ** e == d * (C[0] * p - C[1] * q) * (C[2] * q - C[3] * r) * (C[4] * r - C[5] * p)
assert C[6] * e - C[7] * d == O[3]

n = e * d * p * q * r
m = bytes_to_long(flag)
c = pow(m, 65537, n)
print(f'C = {C}')
print(f'c = {c}')


#C = [5960650533801939766973431801711817334521794480800845853788489396583576739362531091881299990317357532712965991685855356736023156123272639095501827949743772, 6521307334196962312588683933194431457121496634106944587943458360009084052009954473233805656430247044180398241991916007097053259167347016989949709567530079, 1974144590530162761749719653512492399674271448426179161347522113979158665904709425021321314572814344781742306475435350045259668002944094011342611452228289, 2613994669316609213059728351496129310385706729636898358367479603483933513667486946164472738443484347294444234222189837370548518512002145671578950835894451, 8127380985210701021743355783483366664759506587061015828343032669060653534242331741280215982865084745259496501567264419306697788067646135512747952351628613, 5610271406291656026350079703507496574797593266125358942992954619413518379131260031910808827754539354830563482514244310277292686031300804846114623378588204, 10543, 4]
#c = 80607532565510116966388633842290576008441185412513199071132245517888982730482694498575603226192340250444218146275844981580541820190393565327655055810841864715587561905777565790204415381897361016717820490400344469662479972681922265843907711283466105388820804099348169127917445858990935539611525002789966360469324052731259957798534960845391898385316664884009395500706952606508518095360995300436595374193777531503846662413864377535617876584843281151030183895735511854

题解

线性丢番图方程

算法竞赛专题解析（21）：数论–线性丢番图方程 - 罗勇军999 - 博客园 (cnblogs.com)

image-20230710200745942

求解二元一次线性方程，求出e,d

image-20230710185236881

image-20230710201045269

mmexport1688991658703

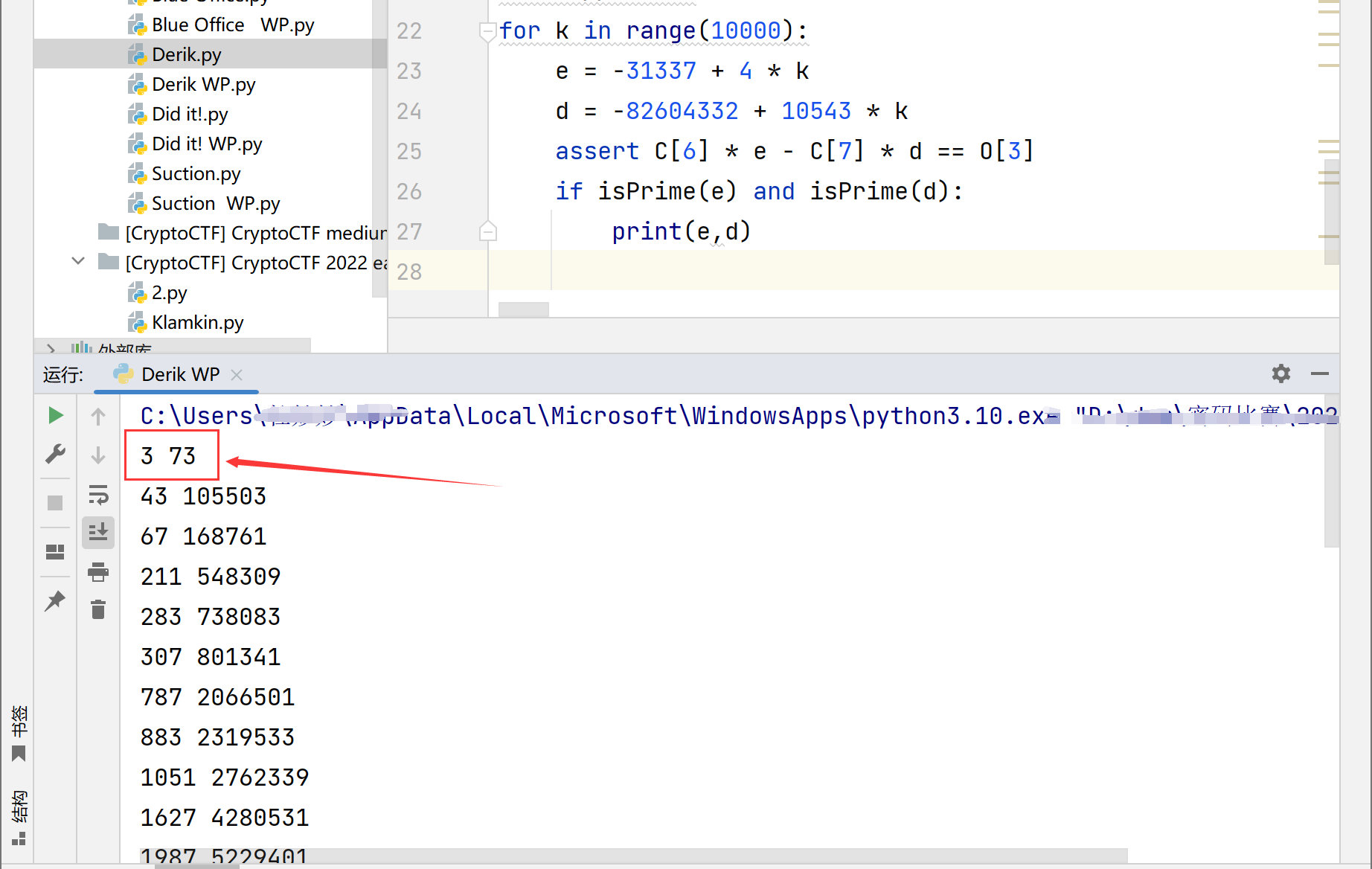
由（1）式推出，当a,b，c比较大时，e的取值比较局限，e,d的一组可能解[3,73]

三次齐次方程等价一个椭圆曲线

R.<x,y,z> = QQ[]
#构造F=0 F=x^3 + y^3 + z^3 - 73 * x * y * z
cubic = x^3 + y^3 + z^3 - 73 * x * y * z
P = [1,-1,0]
#三次齐次方程转化为椭圆曲线
E = EllipticCurve_from_cubic(cubic, P, morphism=False)
#  y^2 - 219*x*y + 3500910*y = x^3 - 47961*x^2 + 766699290*x - 4085456942700

#在椭圆曲线E上找到对应于R的点，并返回该点
f = EllipticCurve_from_cubic(cubic, P, morphism=True)
finv = f.inverse()#逆映射可以用于将椭圆曲线上的点映射回原始定义域，并且保持椭圆曲线上的运算关系。
#R为椭圆曲线对象E的生成元（或基点）。
R = E.gens()[0]
print(finv(R))

#(2848691279889518/1391526622949983 : 89200900157319/1391526622949983 : 1)

结果为(2848691279889518/1391526622949983 : 89200900157319/1391526622949983 : 1)

恢复（x,y,z)=(A,B,C)=(2848691279889518 : 89200900157319 : 1391526622949983)

显然A=O[0],B=O[1],C=O[2]

import gmpy2
from Crypto.Util.number import *

C = [5960650533801939766973431801711817334521794480800845853788489396583576739362531091881299990317357532712965991685855356736023156123272639095501827949743772, 6521307334196962312588683933194431457121496634106944587943458360009084052009954473233805656430247044180398241991916007097053259167347016989949709567530079, 1974144590530162761749719653512492399674271448426179161347522113979158665904709425021321314572814344781742306475435350045259668002944094011342611452228289, 2613994669316609213059728351496129310385706729636898358367479603483933513667486946164472738443484347294444234222189837370548518512002145671578950835894451, 8127380985210701021743355783483366664759506587061015828343032669060653534242331741280215982865084745259496501567264419306697788067646135512747952351628613, 5610271406291656026350079703507496574797593266125358942992954619413518379131260031910808827754539354830563482514244310277292686031300804846114623378588204, 10543, 4]
c = 80607532565510116966388633842290576008441185412513199071132245517888982730482694498575603226192340250444218146275844981580541820190393565327655055810841864715587561905777565790204415381897361016717820490400344469662479972681922265843907711283466105388820804099348169127917445858990935539611525002789966360469324052731259957798534960845391898385316664884009395500706952606508518095360995300436595374193777531503846662413864377535617876584843281151030183895735511854
O = [1391526622949983, 2848691279889518, 89200900157319, 31337]

#print(C[6],C[7])
#10543 4

def ext_euclid(a, b):
    if b == 0:
        return 1, 0, a
    else:
        x, y, q = ext_euclid(b, a % b)
        x, y = y, (x - (a // b) * y)
        return x, y, q
#print(ext_euclid(10543,-4))
#(1, 2636, -1)

#31337//4=7834
for k in range(10000):
    e = -31337 + 4 * k
    d = -82604332 + 10543 * k
    assert C[6] * e - C[7] * d == O[3]
    if isPrime(e) and isPrime(d):
        print(e,d)

image-20230710201916582

题目的O列表中的前3个元素没有用到，猜一下是a,b,c的值

{O[0]=C0∗p−C1∗qO[1]=C2∗q−C3∗rO[2]=C4∗r−C5∗p\begin{cases} O[0]=C_0*p-C1*q\\ O[1]=C_2*q-C3*r\\ O[2]=C_4*r-C5*p \end{cases}

sage解方程组（三个方程，三个未知数）

C = [5960650533801939766973431801711817334521794480800845853788489396583576739362531091881299990317357532712965991685855356736023156123272639095501827949743772, 6521307334196962312588683933194431457121496634106944587943458360009084052009954473233805656430247044180398241991916007097053259167347016989949709567530079, 1974144590530162761749719653512492399674271448426179161347522113979158665904709425021321314572814344781742306475435350045259668002944094011342611452228289, 2613994669316609213059728351496129310385706729636898358367479603483933513667486946164472738443484347294444234222189837370548518512002145671578950835894451, 8127380985210701021743355783483366664759506587061015828343032669060653534242331741280215982865084745259496501567264419306697788067646135512747952351628613, 5610271406291656026350079703507496574797593266125358942992954619413518379131260031910808827754539354830563482514244310277292686031300804846114623378588204, 10543, 4]
p,q,r = var('p q r')
f1 = C[0] * p - C[1] * q - 1391526622949983
f2 = C[2] * q - C[3] * r - 2848691279889518
f3 = C[4] * r - C[5] * p - 89200900157319
solve([f1==0,f2==0,f3==0],p,q,r)

#[[p == 9758621034843917661145412977193922808892309951663464821517963113005483457886774294910761723767526582514514505278091600074371768233672585649562672245905811, q == 8919642442779618620315315582249815126044061421894622037450496385178083791083142991676417756698881509754110765444929271564991855378540939292428839562446571, r == 6736304432663651651650099104581016800112378771266600017972326085742513966258250417227421932482058281545032658577816441378170466639375931780967727070265551]]

wp

from Crypto.Util.number import *
e = 3
d = 73
p = 9758621034843917661145412977193922808892309951663464821517963113005483457886774294910761723767526582514514505278091600074371768233672585649562672245905811
q = 8919642442779618620315315582249815126044061421894622037450496385178083791083142991676417756698881509754110765444929271564991855378540939292428839562446571
r = 6736304432663651651650099104581016800112378771266600017972326085742513966258250417227421932482058281545032658577816441378170466639375931780967727070265551
f = (p-1)*(q-1)*(r-1)*(e-1)*(d-1)
dd = inverse(65537,f)
print(long_to_bytes(pow(c,dd,p*q*r*e*d)))
#b'CCTF{____Sylvester____tHE0r3m_Of_D3r!va7i0n!}'

Insights

题目

#!/usr/bin/env sage
 
from Crypto.Util.number import *
from flag import flag
 
def getRandomNBits(n):
	nb = '1' + ''.join([str(randint(0, 1)) for _ in range(n - 1)])
	return nb
 
def getLeader(L, n):
	nb = L + getRandomNBits(n)
	return int(nb, 2)
 
def genPrime(L, nbit):
	l = len(L)
	assert nbit >= l
	while True:
		p = getLeader(L, nbit - l)
		if is_prime(p):
			return p
 
def genKey(L, nbit):
	p, q = [genPrime(L, nbit) for _ in '__']
	n = p * q
	d = next_prime(pow(n, 0.2919))
	phi = (p - 1) * (q - 1)
	e = inverse(d, phi)
	pubkey, privkey = (n, e), (p, q)
	return pubkey, privkey
 
def encrypt(msg, pubkey):
	n, e = pubkey
	m = bytes_to_long(msg)
	c = pow(m, e, n)
	return c
 
nbit = 1024
L = bin(bytes_to_long(b'Practical'))[2:]
pubkey, privkey = genKey(L, nbit)
p, q = privkey
c = encrypt(flag, pubkey)
 
print('Information:')
print('-' * 85)
print(f'n = {p * q}')
print(f'e = {pubkey[1]}')
print(f'c = {c}')
print(f'p = {bin(p)[2:len(L)]}...[REDACTED]')
print(f'q = {bin(q)[2:len(L)]}...[REDACTED]')
print('-' * 85)

题解

n,e,c已知，给出了d…

wp

from Crypto.Util.number import long_to_bytes

#sage
n = 12765231982257032754070342601068819788671760506321816381988340379929052646067454855779362773785313297204165444163623633335057895252608396010414744222572161530653104640020689896882490979790275711854268113058363186249545193245142912930804650114934761299016468156185416083682476142929968501395899099376750415294540156026131156551291971922076435528869024742993840057342092865203064721826362149723366381892539617642364692012936270150691803063945919154346756726869466855557344213050973081755499746750276623648407677639812809665472258655462846021403503851719008687214848550916999977775070011121527941755954255781343103086789
e = 459650454686946706615371845737527916539205656667844780634386049268800615782964920944229084502752167395446158290854047696006034750210758341744841762479191173017773034647739346927390580848998121830029134542880713409306092967282675122699586503684943407535067216738556403169403622104762516293879994387324370835718056251706150557820106296417750402984941838652433642298378976899556042987560946508887315484380807248331504458640857234708123277403252632993828101306072382329879857946191508782246793011691530554606521701055094223574951862129713872918021549814674387049788995785872980320871421550616327471735316980754238323013
c = 10992248752412909788626396175372747713079469256270100576886987393986576680666320383209810005318254336440105142571546847427454822405793626080251363454531982746373841267986148332456716023293306870382809568309620264499225135226626560298741596462262513921032733814032790312163314776421380481083058518893602887082464123177575742160690315666730642727773288362853901330620841098230284739614618790097180848133698381487679399364400048499041582830157094876815030301231505774900176910650887780842536610942820066913075027528705150102760422836458745949063992228680293226303245265232017738712226154128654682937687199768621565945171

d = next_prime(int(pow(n, 0.2919)))
m = pow(c,d,n)
long_to_bytes(int(m))
#CCTF{RSA_N3w_rEc0rd5_4Nd_nEw_!nSi9h75!}

ASIv1

题目

#!/usr/bin/env python3
 
from Crypto.Util.number import *
from flag import flag
 
def base(n, l):
    D = []
    while n > 0:
        n, r = divmod(n, l)
        D.append(r)
    return ''.join(str(d) for d in reversed(D)) or '0'
 
def asiv_prng(seed):
	l = len(seed)
	_seed = base(bytes_to_long(seed), 3)
	_seed = [int(_) for _ in _seed]
	_l = len(_seed)
	R = [[getRandomRange(0, 3) for _ in range(_l)] for _ in range(_l**2)]
	S = []
	for r in R:
		s = 0
		for _ in range(_l):
			s += (r[_] * _seed[_]) % 3
		# s += getRandomRange(0, 3)
		s %= 3
		S.append(s)
	return R, S
 
seed = flag.lstrip(b'CCTF{').rstrip(b'}')
R, S = asiv_prng(seed)
 
f = open('output.txt', 'w')
f.write(f'R = {R}\nS = {S}')
f.close()

题解

S=R∗flag  (mod  3)S=R*flag \ \ (mod \ \ 3)

矩阵求解sage

image-20230711191532469

IMG20230711202457

WP


#sage
file = open('D:\\浏览器下载\\刷题附件\\output.txt', 'r')
# 读取文件内容
content = file.read()
file.close()

# 提取R的值
start1 = content.find('R = [') + len('R = ')
#print(start1)
end1 = content.find(']]', start1)
R = content[start1:end1+2]
R = eval(R)
start2 = content.find('S = [') + len('S = ')
#print(start2)
end2 = content.find(']', start2)
S = content[start2:end2+1]
S = eval(S)

#print(R)
#print(S)
#将列表R转换为一个在这个有限域上的矩阵MR
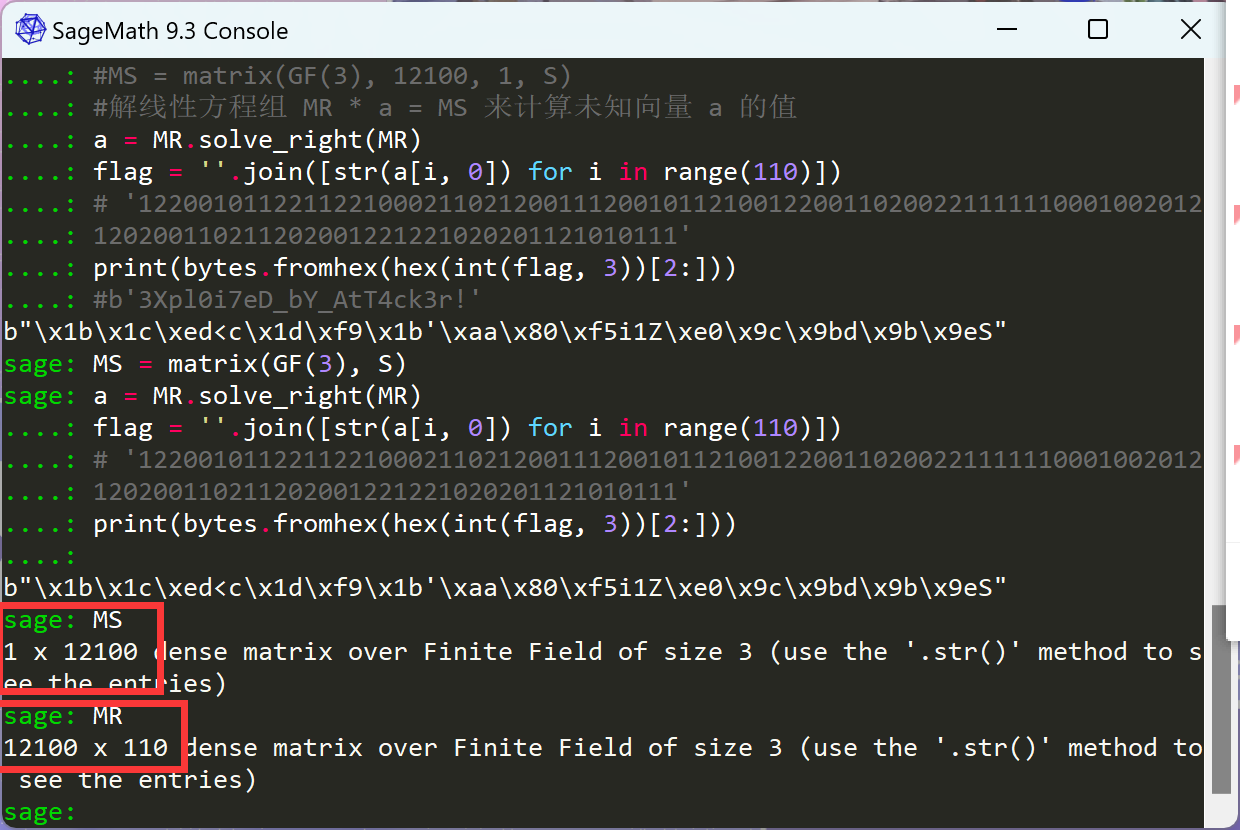
MR = matrix(GF(3), R)
#转化为一维矩阵（向量）
MS = matrix(GF(3), 12100, 1, S)
a = MR.solve_right(MR)
flag = ''.join([str(a[i, 0]) for i in range(110)])
print(bytes.fromhex(hex(int(flag, 3))[2:]))
#b'3Xpl0i7eD_bY_AtT4ck3r!'

Resuction

题目

Handmade and artificial resuction cryptosystems represent contrasting approaches to encryption: while handmade systems emphasize the meticulous craftsmanship and personalization of cryptographic algorithms, artificial resuction systems rely on machine-generated algorithms that are optimized through computational techniques.

#!/usr/bin/env python3

from Crypto.Util.number import *
from flag import flag

from decimal import *

def keygen(nbit, r):
	while True:
		p, q = [getPrime(nbit) for _ in '__']
		d, n = getPrime(64), p * q
		phi = (p - 1) * (q - 1)
		if GCD(d, phi) == 1:
			e = inverse(d, phi)
			N = bin(n)[2:-r]
			E = bin(e)[2:-r]
			PKEY = N + E
			pkey = (n, e)
			return PKEY, pkey

def encrypt(msg, pkey, r):
	m = bytes_to_long(msg)
	n, e = pkey
	c = pow(m, e, n)
	C = bin(c)[2:-r]
	return C

r, nbit = 8, 1024
PKEY, pkey = keygen(nbit, r)
print(f'PKEY = {int(PKEY, 2)}')
FLAG = flag.lstrip(b'CCTF{').rstrip(b'}')
enc = encrypt(FLAG, pkey, r)
print(f'enc = {int(enc, 2)}')

'''
PKEY = 14192646310719975031517528381795548241077678859071194396837281472399230674325587198691913743313024193030641258581477544395982020385534616950314446352119543012689979705497443206671093873748633162188213109347667494028713308821945628880987033909436936504594085029207071182583896573425433818693447573712242776054326253393149643818428222532313129014785625379928796322492111783102063504659053965652092334907431265629283336869752591405010801363428649651892548988084920295512198406822149854508798413366425646089176325412867633899847841343293434518769693835679828109184625256833518392375615524221729773443578746961887429674099018040291053535429314874943299587513900900515776980848746070077651676814430155460898107362207677739452859298842563030631706907437662807884529549746843462830493900480079096937402325307522965877069080418178692616875205678928420840955518031258855869218152431304423803589723140983606576549207164114711076498723237274262054605174412193097533550076687418481230734706280737017543741247718967059747548710091320650704988384742281590019869955579949961574733610565593105027342454880292474482792325237942870408329807427182014062811782475262070063065860763705715879581562335668163076088547827008755841277828137570366416095778
enc = 93313196155732054514477836642637636744872135106456047659057794344503071105783322399713135615723000054324693644981340568454628360027598469597864407205974007198804288563284521413279406211756674451582156555173212403946908121125010635246043311803494356106191509999360722019559999844621905376368824621365540442906142224342650371557766313381899279520110833822291649001754956653102495882094754863493058001964760438040783400782352466943990226083197340594364084294954324101604417550048379969516185353765224920719355485680872367930581872987972421836853197205534334204586713387469939986387582911728909524428102693874671302382

'''

题解

和suction很像，但这里给出的是d–>64位，而且p,q是1024位

p,q是1024位，n大概2048位，nh=2040位

bitsequence = f'{PKEY:b}'
N, e = bitsequence[:2040], bitsequence[2040:]
print(len(N))
print(len(e))
2040
2040

nh=2040位，eh=2040位

{e=eh+(0,28)  e≈ehn=nh+(0,28)  n≈nh\begin{cases} e=eh+(0,2^8)\ \ e\approx eh\\ n=nh+(0,2^8)\ \ n\approx nh\\ \end{cases}

由于d很大，维纳攻击，通过n,e的高位求出d

爆破n,e、

c≡me(modn)m≡cd(modn)cd≡med≡m(modn)通过ted≡t(modn)来验证n,ec\equiv m^e(mod n)\\ m\equiv c^d(mod n)\\ c^d\equiv m^ed\equiv m(mod n)\\ 通过 t^ed\equiv t(mod n)来验证n,e 

if pow(2, e*d, n) == 2:

求出n,e,d后，爆破c，通过“CCTF”筛选 m

wp

from Crypto.Util.number import long_to_bytes
from rsa.prime import is_prime

from tqdm import tqdm
PKEY = 14192646310719975031517528381795548241077678859071194396837281472399230674325587198691913743313024193030641258581477544395982020385534616950314446352119543012689979705497443206671093873748633162188213109347667494028713308821945628880987033909436936504594085029207071182583896573425433818693447573712242776054326253393149643818428222532313129014785625379928796322492111783102063504659053965652092334907431265629283336869752591405010801363428649651892548988084920295512198406822149854508798413366425646089176325412867633899847841343293434518769693835679828109184625256833518392375615524221729773443578746961887429674099018040291053535429314874943299587513900900515776980848746070077651676814430155460898107362207677739452859298842563030631706907437662807884529549746843462830493900480079096937402325307522965877069080418178692616875205678928420840955518031258855869218152431304423803589723140983606576549207164114711076498723237274262054605174412193097533550076687418481230734706280737017543741247718967059747548710091320650704988384742281590019869955579949961574733610565593105027342454880292474482792325237942870408329807427182014062811782475262070063065860763705715879581562335668163076088547827008755841277828137570366416095778
enc = 93313196155732054514477836642637636744872135106456047659057794344503071105783322399713135615723000054324693644981340568454628360027598469597864407205974007198804288563284521413279406211756674451582156555173212403946908121125010635246043311803494356106191509999360722019559999844621905376368824621365540442906142224342650371557766313381899279520110833822291649001754956653102495882094754863493058001964760438040783400782352466943990226083197340594364084294954324101604417550048379969516185353765224920719355485680872367930581872987972421836853197205534334204586713387469939986387582911728909524428102693874671302382
c=enc<<8
bitsequence = f'{PKEY:b}'
N, e = bitsequence[:2040], bitsequence[2040:]
print(len(N))
print(len(e))
N, e = map(lambda x: int(x, 2), (N, e))
#print(N,e)
nh=N<<8
eh=e<<8


def continuedFra(x, y):
    """计算连分数
    :param x: 分子
    :param y: 分母
    :return: 连分数列表
    """
    cf = []
    #辗转相除法
    while y:
        cf.append(x // y)
        x, y = y, x % y
    return cf
def gradualFra(cf):
    """计算传入列表最后的渐进分数
    :param cf: 连分数列表
    :return: 该列表最后的渐近分数
    """
    numerator = 0#分子
    denominator = 1#分母
    for x in cf[::-1]:
        # 这里的渐进分数分子分母要分开
        numerator, denominator = denominator, x * denominator + numerator
    return numerator, denominator

def getGradualFra(cf):
    """计算列表所有的渐近分数
    :param cf: 连分数列表
    :return: 该列表所有的渐近分数
    """
    gf = []
    for i in range(1, len(cf) + 1):
        gf.append(gradualFra(cf[:i]))
    return gf

cf = continuedFra(eh, nh)#获得连分数列表
for (d0, k) in getGradualFra(cf):#所有渐进分数
    if d0.bit_length() == 64 and is_prime(d0):
        d=d0
        break

print(d)

#爆破n,e,
for i in tqdm(range(2**8)):
    for j in  range(2**8):
        for k in range(2**8):
            n = nh + i
            e = eh + j
            if pow(2, e*d, n) == 2:
                #print(f'n = {n}')
                #print(f'e = {e}')
                c=c+k
                m=pow(c,d,n)
                m=long_to_bytes(m)
                if b'CCTF{' in m:
                    print(m)
#n = 28781418259071163834545208786492597316357138268450456443121779857237190669654679502925616925907115061139426651454246296829614929839091896732956124186768298711851015827257060255218333952539548249210858753648965921585289379414151961197198777686222970660319202167442420274437451557166736926361972983650143650097981777542950972139757680517744639660898696901009088978971506526002932830312595664154921938706240176536981793499426543601513874115451315768319593051858239793153849410530285884330866972048864103208648273010126369559341912163849839663249252300813799486995834473605326584986843653735963725697383056972744506296271
#e = 19152712448778858582528734875468196678366984818842265525346340114296810907435357813959451387293270496095878944786775775749129832803842508074794234774568097809721690831345120778762600713106116293626590641716601095020202233532544196547654794913903350183891867544539554967347396716482565232986995497267273877597593761608770699282404807896050347585632153075234094034163801474316224123620090879021107631960008144066862084573910442635526649884938724881478713853362879412453150893601267748827792136092224063120914443976032390554506925020506643629449426005820918745312311984391868895996772772355715765028825561022860823765675

'''           

'''

Roldy

题目

Roldy,once regarded as a reliable cryptosystem library, has unfortunately emerged as one of the most vulnerable and compromised systems in recent times, leaving users exposed to significant security risks.

#!/usr/bin/env python3

from Crypto.Util.number import *
from pyope.ope import OPE as enc
from pyope.ope import ValueRange
import sys
from secret import key, flag

def die(*args):
	pr(*args)
	quit()

def pr(*args):
	s = " ".join(map(str, args))
	sys.stdout.write(s + "\n")
	sys.stdout.flush()

def sc():
	return sys.stdin.buffer.readline()

def encrypt(msg, key, params):
	if len(msg) % 16 != 0:
		msg += (16 - len(msg) % 16) * b'*'
	p, k1, k2 = params
	msg = [msg[_*16:_*16 + 16] for _ in range(len(msg) // 16)]
	m = [bytes_to_long(_) for _ in msg]
	inra = ValueRange(0, 2**128)
	oura = ValueRange(k1 + 1, k2 * p + 1)
	_enc = enc(key, in_range = inra, out_range = oura)
	C = [_enc.encrypt(_) for _ in m]
	return C

def main():
	border = "|"
	pr(border*72)
	pr(border, " Welcome to Roldy combat, we implemented an encryption method to    ", border)
	pr(border, " protect our secret. Please note that there is a flaw in our method ", border)
	pr(border, " Can you examine it and get the flag?                               ", border)
	pr(border*72)

	pr(border, 'Generating parameters, please wait...')
	p, k1, k2 = [getPrime(129)] + [getPrime(64) for _ in '__']
	C = encrypt(flag, key, (p, k1, k2))

	while True:
			pr("| Options: \n|\t[E]ncrypted flag! \n|\t[T]ry encryption \n|\t[Q]uit")
			ans = sc().decode().lower().strip()
			if ans == 'e':
				pr(border, f'encrypt(flag, key, params) = {C}')
			elif ans == 't':
				pr(border, 'Please send your message to encrypt: ')
				msg = sc().rstrip(b'\n')
				if len(msg) > 64:
					pr(border, 'Your message is too long! Sorry!!')
				C = encrypt(msg, key, (p, k1, k2))
				pr(border, f'C = {C}')
			elif ans == 'q':
				die(border, "Quitting ...")
			else:
				die(border, "Bye ...")

if __name__ == '__main__':
	main()

题解

加密基于ECB模式的分组加密，pyope包中的OPE加密算法。

不会

wp

[CryptoCTF] CryptoCTF 2023 medium分类 团队解题writeup 之二 - 知乎 (zhihu.com)

TPSD

题目

Solving Diophantine equations is a notoriously challenging problem in number theory, and finding non-trivial integer solutions for certain equations is considered a major open problem in mathematics.

image-20230711215203859

题解

(15 封私信 / 80 条消息) 该怎么解决下面这个不定方程？ - 知乎 (zhihu.com)

解决

p∗∗3+q∗∗3+r∗∗3=1p**3+q**3+r**3=1

其中p,q,r中至少有一个素数，且最小值是9-29bit

image-20230711220643841

image-20230711221134532

令b=2∗a，  此时w=c∗4只要遍历c即可令b=2*a，\ \ 此时w=c*4\\只要遍历c即可

找到某个比特范围内的解（x,y,x)，只需要对a进行合理取值，即 a = random.getrandbits(nn)

nn=bits//3 (因为d = c * (a ** 3 + (a - b) ** 3 + c ** 3))

wp

from pwn import *
from Crypto.Util.number import *
import random

def attack(nn,l,h):
    while True:

        a = random.getrandbits(nn)
        # 假定a和b的关系
        # w为1
        b = 2 * a
        for c in range(1, 4):
            d = c * (a ** 3 + (a - b) ** 3 + c ** 3)
            if c * (-1 * a ** 3 - b ** 3 + c ** 3) % d == 0 and (
                    -1 * (a ** 2 - a * b + b ** 2) ** 2 + (a + b) * c ** 3) % d == 0 and (
                    (a ** 2 - a * b + b ** 2) ** 2 + (2 * a - b) * c ** 3) % d == 0:
                temp_x = c * (-1 * a ** 3 - b ** 3 + c ** 3) // d
                temp_y = (-1 * (a ** 2 - a * b + b ** 2) ** 2 + (a + b) * c ** 3) // d
                temp_z = ((a ** 2 - a * b + b ** 2) ** 2 + (2 * a - b) * c ** 3) // d
                assert temp_x ** 3 + temp_y ** 3 + temp_z ** 3 == 1
                x, y, z = (abs(temp_x), abs(temp_y), abs(temp_z))
                if (isPrime(x) or isPrime(y) or isPrime(z)) and min(x, y, z).bit_length() >= l and min(x, y, z).bit_length() <= h:
                    return (temp_x, temp_y, temp_z)
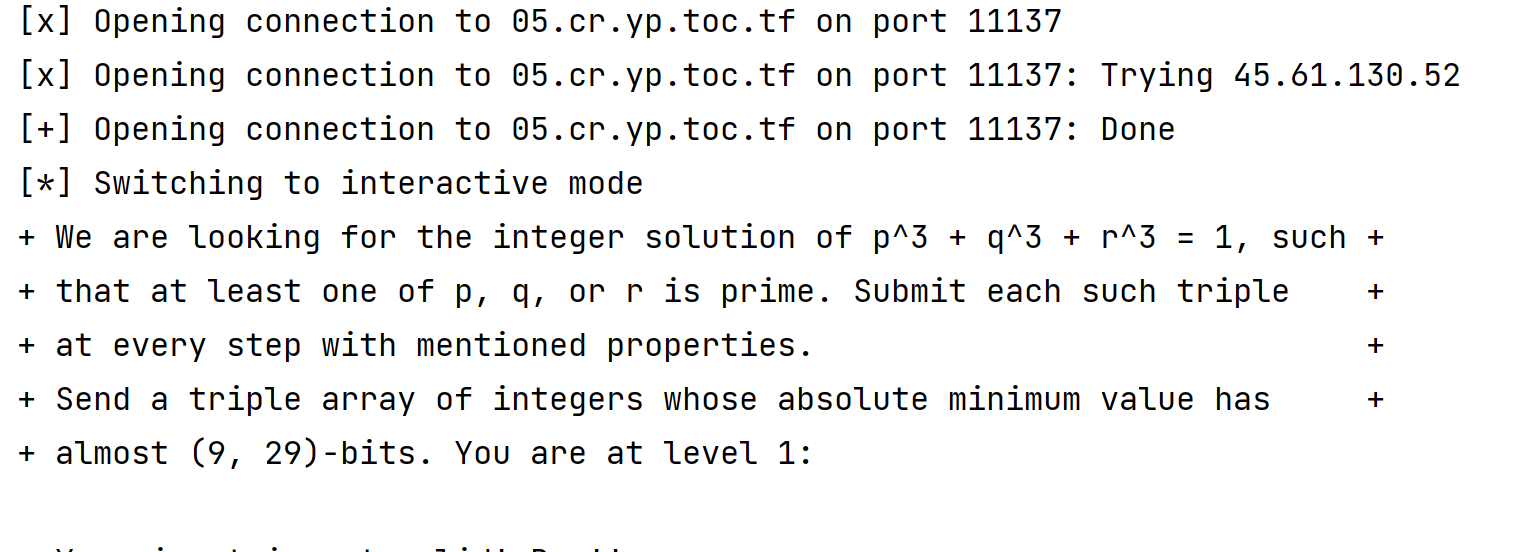
io = remote('05.cr.yp.toc.tf',11137)
print(io.recvuntil(b'value has     +\n'))
re=io.recvline()
print(re)
p1 = re.find(b'(')
p2 = re.find(b',')
p3 = re.find(b')')
l = int(re[p1+1:p2])
h = int(re[p2+2:p3])
print(l,h)
nn = l // 3
ans = attack(nn, l, h)
io.sendline(str(ans)[1:-1].encode())
#io.interactive()
for i in range(50):
    if i == 18:
        io.interactive()
    rev = io.recvlines(3)
    print(rev)
    #找到最低bits -- l,和最高bits--h
    p1 = rev[2].find(b'(')
    p2 = rev[2].find(b',')
    p3 = rev[2].find(b')')
    l = int(rev[2][p1+1:p2])
    h = int(rev[2][p2+2:p3])
    print(l,h)
    nn = l//3
    ans = attack(nn,l,h)
    print(ans)
    io.sendline(str(ans)[1:-1].encode())

    #CCTF{pr1m3S_in_7ErnArY_Cu8!c_3qu4tI0nS!}

Trex

题目

The study of Diophantine equations over trex can be significantly more challenging than over the real numbers.

#!/usr/bin/env python3

import random
import sys
from flag import flag

def die(*args):
	pr(*args)
	quit()

def pr(*args):
	s = " ".join(map(str, args))
	sys.stdout.write(s + "\n")
	sys.stdout.flush()

def sc():
	return sys.stdin.buffer.readline()

def check_inputs(a, b, c):
	if not all(isinstance(x, int) for x in [a, b, c]):
		return False
	if a == 0 or b == 0 or c == 0:
		return False
	if a == b or b == c or a == c:
		return False
	return True

def check_solution(a, x, y, z):
	return (x*x + y*y - x*y - a*(z**3)) == 0

def main():
	border = "|"
	pr(border*72)
	pr(border, ".::   Hi all, she DID it, you should do it too! Are you ready? ::.  ", border)
	pr(border, "Welcome to the Ternary World! You need to pass each level until 20  ", border)
	pr(border, "to get the flag. Pay attention that your solutions should be nonzero", border)
	pr(border, "distinct integers. Let's start!                                     ", border)
	pr(border*72)

	level, step = 0, 19
	while level <= step:
		a = random.randint(2**(level * 12), 2**(level*12 + 12))
		equation = f'x^2 + y^2 - xy = {a}*z^3'
		pr(f"Level {level + 1}: {equation}")
		inputs = input().strip().split(",")
		try:
			x, y, z = map(int, inputs)
		except:
			die(border, "Invalid input, Bye!!")
		if check_inputs(x, y, z):
			if check_solution(a, x, y, z):
				pr(border, "Correct! Try the next level :)")
				level += 1
			else:
				pr(border, "You didn't provide the correct solution.")
				die(border, "Better luck next time!")			
		else:
			pr(border, "Your solutions should be non-zero distinct integers")
			die(border, "Quiting...")
		if level == step:
			pr(border, "Congratulations! You've successfully solved all the equations!")
			die(border, f"flag: {flag}")

if __name__ == '__main__':
	main()

题解

尝试19轮，解下述等式

x2+y2−x∗y=a∗z3x^2+y^2-x*y=a*z^3

令

{x=m∗a2y=n∗a2z=l∗a     代入可得   m2+n2−m∗n=l3\begin{cases} x=m*a^2\\ y=n*a^2\\z=l*a \end{cases}\\ \ \ \ \ \ 代入可得 \ \ \ m^2+n^2-m*n=l^3

消去a，找到一组解

{m=3n=6l=3  代入可得解{x=3∗a2y=6∗a2z=3∗a\begin{cases} m=3\\ n=6\\l=3 \end{cases}\\ \ \ 代入可得解 \begin{cases} x=3*a^2\\ y=6*a^2\\z=3*a \end{cases}\\

wp

from pwn import *

def attack(a):
    x=3*a**2
    y=6*a**2
    z=3*a
    return (x,y,z)

io = remote('03.cr.yp.toc.tf',31317)
banner = io.recvlines(6)
print(banner)
l1 = banner[-1]
print(l1)
#读取a值
p1 = l1.find(b'= ')
p2 = l1.find(b'*')
a = int(l1[p1+2:p2])
print(a)
ans1 = attack(a)
print(ans1)
io.sendline(str(ans1)[1:-1].encode())

for i in range(18):
    print(f'第{i}次')
    rev = io.recvlines(2)
    print(rev)
    l = rev[-1]
    p1 = l.find(b'= ')
    p2 = l.find(b'*')
    a = int(l[p1 + 2:p2])
    #print(a)
    ans = attack(a)
    #print(ans)
    io.sendline(str(ans)[1:-1].encode())

io.interactive()
io.close()

#CCTF{T3rn3ry_Tr3x_3Qu4t!0n}

Keymoted

题目

Combining RSA and ECC in a cryptographic system does not necessarily guarantee security equivalent to that of the individual RSA or ECC systems. What about keymoted


#!/usr/bin/env sage

from Crypto.Util.number import *
from flag import flag

def gen_koymoted(nbit):
	p = getPrime(nbit)
	a, b = [randint(1, p - 1) for _ in '__']
	Ep = EllipticCurve(GF(p), [a, b])
	tp = p + 1 - Ep.order()
	_s = p ^^ ((2 ** (nbit - 1)) + 2 ** (nbit // 2))
	q = next_prime(2 * _s + 1)
	Eq = EllipticCurve(GF(q), [a, b])
	n = p * q
	tq = q + 1 - Eq.order()
	e = 65537
	while True:
		if gcd(e, (p**2 - tp**2) * (q**2 - tq**2)) == 1:
			break
		else:
			e = next_prime(e)
	pkey, skey = (n, e, a, b), (p, q)
	return pkey, skey

def encrypt(msg, pkey, skey):
	n, e, a, b = pkey
	p, q = skey
	m = bytes_to_long(msg)
	assert m < n
	while True:
		xp = (m**3 + a*m + b) % p
		xq = (m**3 + a*m + b) % q
		if pow(xp, (p-1)//2, p) == pow(xq, (q-1)//2, q) == 1:
			break
		else:
			m += 1
	eq1, eq2 = Mod(xp, p), Mod(xq, q)
	rp, rq = sqrt(eq1), sqrt(eq2)
	_, x, y = xgcd(p, q)
	Z = Zmod(n)
	x = (Z(rp) * Z(q) * Z(y) + Z(rq) * Z(p) * Z(x)) % n
	E = EllipticCurve(Z, [a, b])
	P = E(m, x)
	enc = e * P
	return enc

nbit = 256
pkey, skey = gen_koymoted(nbit)
enc = encrypt(flag, pkey, skey)

print(f'pkey = {pkey}')
print(f'enc = {enc}')


#pkey = (6660938713055850877314255610895820875305739186102790477966786501810416821294442374977193379731704125177528590285016474818841859956990486067573436301232301, 65537, 5539256645640498184116966196249666621079506508209770360679460869295427007578, 20151017657582479433586370393795140515103572865771721775868586710594524816458)
#enc = (6641320679869421443758875467781930795132746694454926965779628505713445486895274490835545942727970688359873955019634877304270220728625521646208912044469433 : 2856872654927815636828860866843721158889474116106462420201092148493803550131351543372740950198853438539317164093538508795630146854596724019329887894933972 : 1)

题解

wp