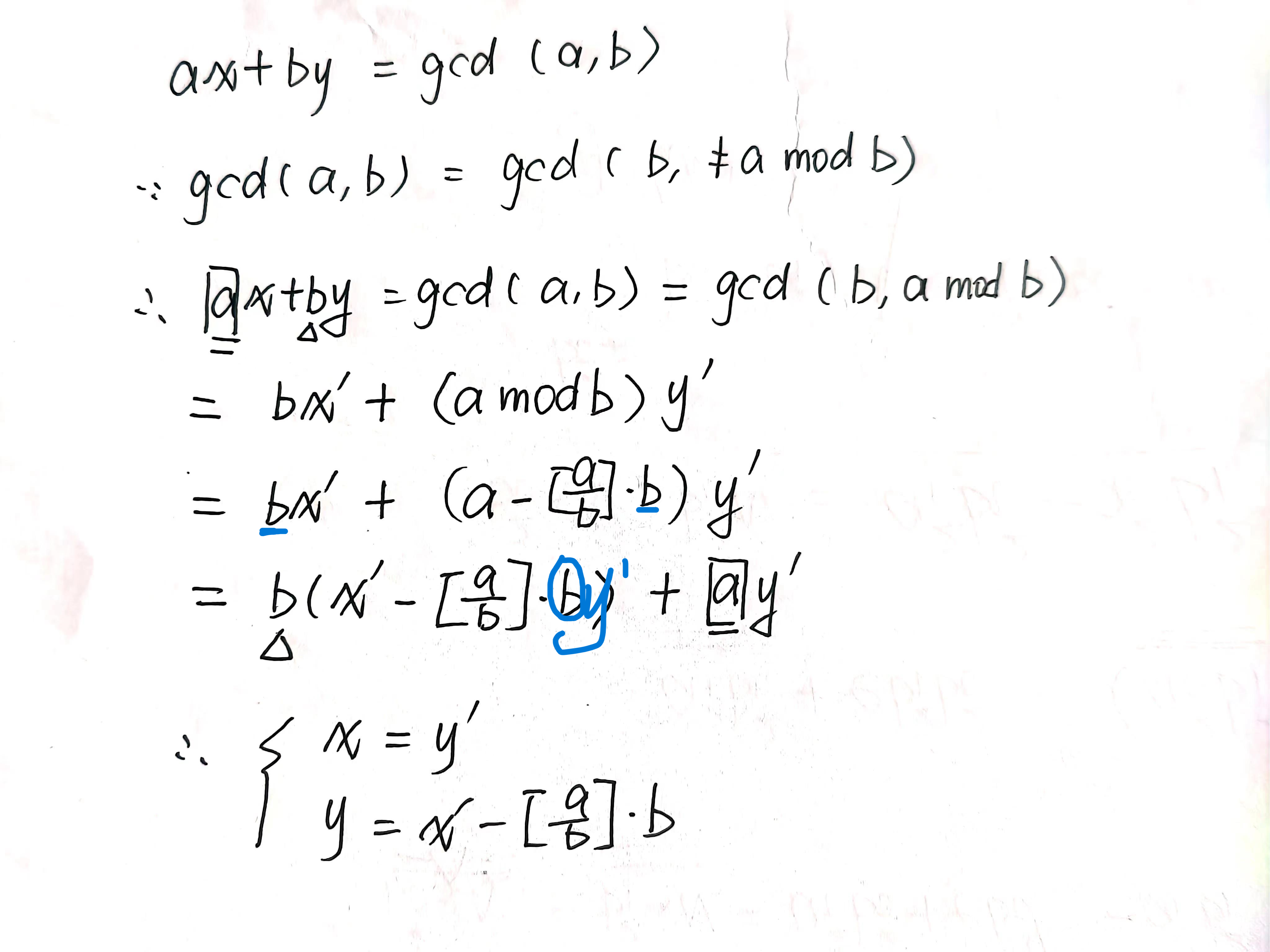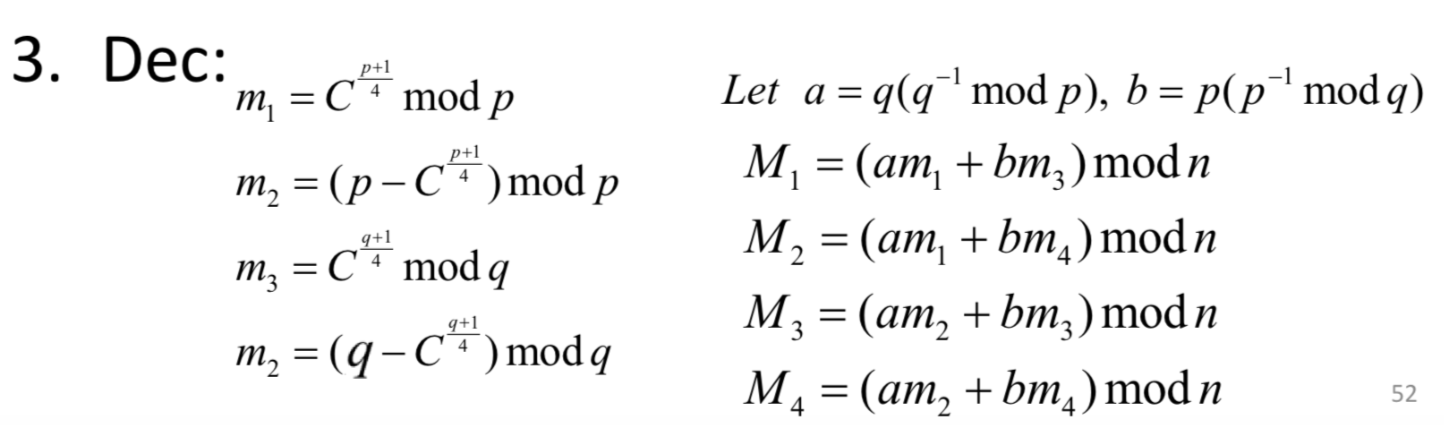密码数论基础

基础数论

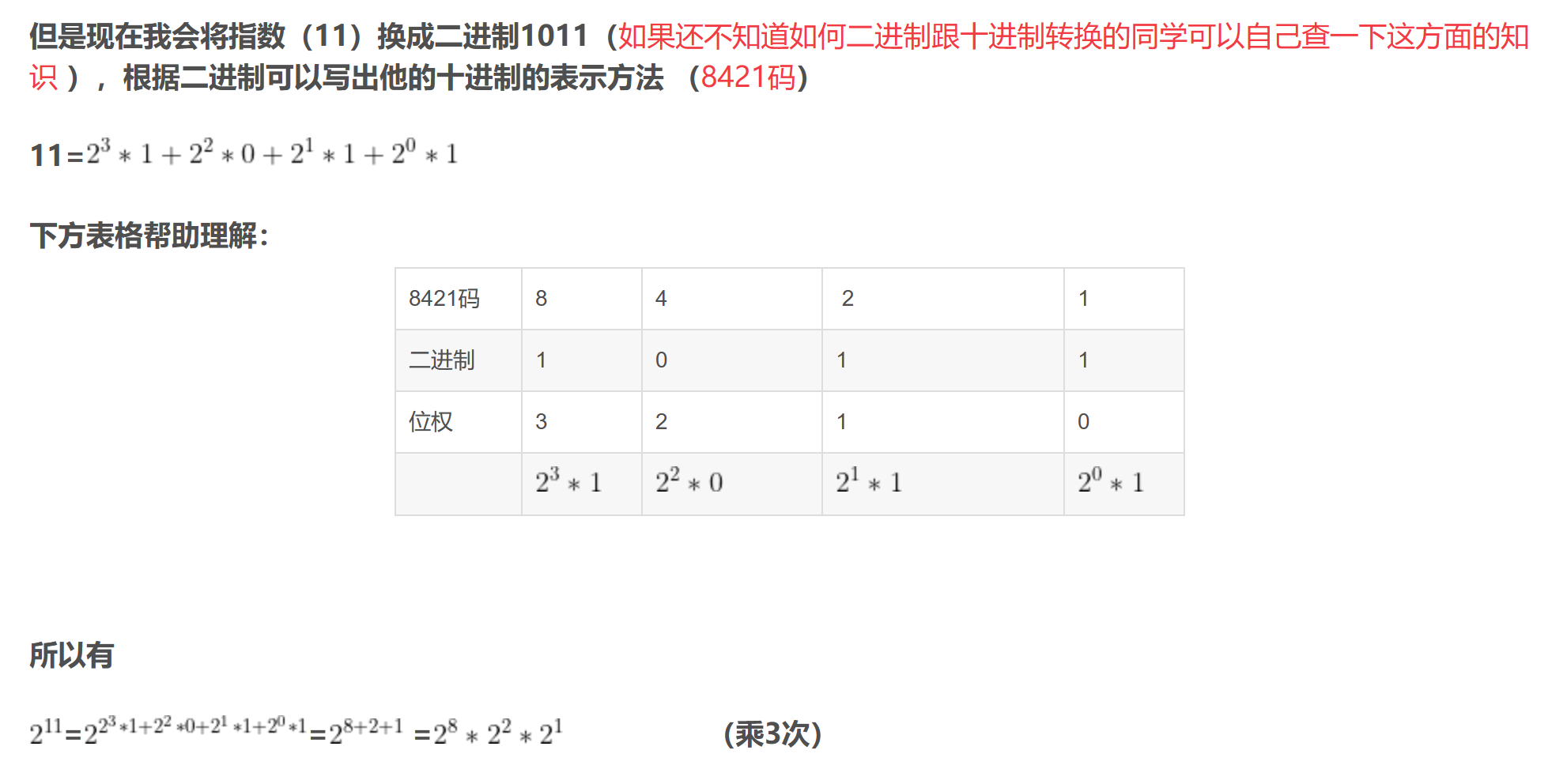
#  &用于取位操作，例如（x&1）的结果是将十进制数（x）转换成二进制数之后再取最后一位
def fastPower(int base, int exponent) {
    int sum = 1;
    while (exponent != 0) { 
        #&取二进制末尾
        if ((exponent & 1) != 0) {
            #实现2^8*2^2*2^1
            sum *= base;
        }
     # 对指数进行移位 1011->0101->0010->0000
     exponent = expnonent >> 1; 
     # 让base的次幂以2的倍数增长   实现base->base^2->base^4->base^8
     base *= base;         
    }
    return sum;
}

2.折半

def quik_power(int base, int power)
{
	result = 1
    #指数大于0进行指数折半，底数变其平方的操作
	while power > 0:         
	{
        #指数为奇数，power & 1这相当于power % 2 == 1
		if power & 1:
          #分离出当前项并累乘后保存
			result *= base;  
        #指数折半,power >>= 1这相当于power /= 2;
		power >>= 1;
     #底数变其平方
		base *= base;         
	}
	return result;       
}

中国剩余定理

#联立两个同余方程
import gmpy2
def shengyu(a1,a2,m1,m2):
    M=m1*m2
    M1=M//m1
    M2=M//m2
    t1=gmpy2.invert(M1)
    t2=gmpy2.invert(M2)
    x1=(a1*M1*t1)%M
    x2=(a2*M2*t2)%M
    return (x1+x2)%M

拓展欧几里得定理

def ext_gcd(a, b): #扩展欧几里得算法
    if b == 0:
        return 1, 0, a
    else:
        x, y, gcd = ext_gcd(b, a % b) #递归直至余数等于0(需多递归一层用来判断)
        x, y = y, (x - (a // b) * y) 
        return x, y, gcd

求乘法逆元

1.费马定理

$a^{(p-1)}\equiv 1 ( mod p)$

前提：a是不能被指数整除的正整数

$a*a^{(p-2)}\equiv 1(mod p)$

所以a的逆元是

$a^{(p-2)}$

#费马求a关于b的逆元
def niyuan(a,p):
    ret=1
    b=p-2
    while b:
        if b&1:
            ret=(ret*a)%p
        a=(a*a)%p
        b>>=1
    return ret

2.拓展欧几里得

拓展欧几里得用于求出关于x,y的方程的一组整数解

当gcd(a,b)=1时，有

$ax\equiv1 (mod p)$

$等价于 ax+kp\equiv1$

a,p互质

# 扩展欧几里得求a关于p的逆元
#逆元：a，p需要互质
#拓展欧几里得
def exgcd(a, b):
    if b == 0:
        return 1, 0, a
    else:
        x, y, q = exgcd(b, a % b)
        x, y = y, (x - (a // b) * y)
        return x, y, q


def ModReverse(a,p):
    x, y, q = exgcd(a,p)
    if q != 1:
        #a,p互质
        raise Exception("No solution.")
    else:
        return (x + p) % p #防止负数

利用数论解决rabin

Rabin加密

选取两个素数p,q，两个都同余3模4，p,q作为私钥，N=p*q作为公钥

ENC:加密一个消息M<n,C=M^2 mod n

Dec:

Rabin解密

import gmpy2
n =
p=
q=
d =
e =2
c = 

c1=pow(c,(p+1)/4,p)
c2=pow(c,(q+1)/4,q)
cp1=p-c1
cp2=q-c2
t1=gmpy2.invert(p,q)#p的模q逆元
t2=gmpy2.invert(q,p)#q的模p逆元

#中国剩余定理
m1=(q*c1*t2+p*c2*t1)%n
m2=(q*c1*t2+p*cp2*t1)%n # or m2=n-m1
m3=(q*cp1*t2+p*c2*t1)%n
m4=(q*cp1*t2+p*cp2*t1)%n # or m4=n-m3

for i in(m1,m2,m3,m4):
    m = '%x' % i
    if len(m)%2==1:
        m='0'+m 
    print(m.decode('hex'))